Question

In a pollution study of 1500 Indian rivers, the following data were reported. 520 were polluted by sulphur compounds, 335 polluted by phosphate, 425 were polluted by crude oil, 100 were polluted by both crude oil and sulphur compounds, 180 were polluted by both sulphur compounds and phosphates, 150 were polluted by both phosphates and crude oil and 28 were polluted by sulphur compounds, phosphates, and crude oil. \[\]
How many of the rivers were polluted by exactly one on the three impurities? \[\]
A.510 \[\]
B.504 \[\]
C.205 \[\]
D.405 \[\]

Answer 1

Hint: We denote the set of rivers polluted by sulphur, by phosphate and by crude oil as $S,P,C$ respectively. We draw the Venn’ diagram and see that the number of rivers polluted by only sulphur is $n\left( S \right)-n\left( C\bigcap S \right)-n\left( S\bigcap P \right)+n\left( S\bigcap C\bigcap P \right)$, the number of rivers polluted by only sulphur is $n\left( P \right)-n\left( C\bigcap P \right)-n\left( S\bigcap P \right)+n\left( S\bigcap C\bigcap P \right)$, the number of rivers polluted by only crude oil is $n\left( C \right)-n\left( C\bigcap S \right)-n\left( C\bigcap P \right)+n\left( S\bigcap C\bigcap P \right)$. We add them to get the result. \[\]

Complete step by step answer:
Let us denote the set of rivers polluted by sulphur, phosphate, and by crude oil as $S,P, C$ respectively. We are given that a pollution study has been done on of 1500 Indian rivers. So we take the cardinality of the union of river seta and have;
\[n\left( S\bigcup P\bigcup C \right)=1500\]
We are further given 520 rivers were polluted by sulphur compounds, 335 rivers polluted by phosphate, 425 rivers were polluted by crude oil. So we have;
\[n\left( S \right)=520,n\left( P \right)=335,n\left( C \right)=425\]
We are further given that 100 rivers were polluted by both crude oil and sulphur compounds, 180 rivers were polluted by both sulphur compounds and phosphates, 150 rivers were polluted by both phosphates and crude oil. So we have;
$n\left( C\bigcap S \right)=100,n\left( S\bigcap P \right)=180,n\left( C\bigcap P \right)=150$
We are further given rivers were polluted by sulphur compounds, phosphates, and crude oil. So we have;
$n\left( S\bigcap P\bigcap C \right)=28$
Let us draw the Venn diagram.

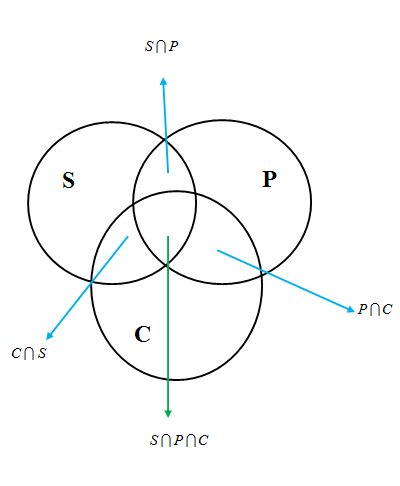
Let us first find the number rivers polluted by only sulphate. So here we have to exclude the regions $S\bigcap P,C\bigcap S$from the circle of S but when we do that the region of $S\bigcap P\bigcap C$ is removed twice, so we have to include the region of $S\bigcap P\bigcap C$ once . So the number of rivers polluted by only sulphate is
\[n\left( S \right)-n\left( C\bigcap S \right)-n\left( S\bigcap P \right)+n\left( S\bigcap C\bigcap P \right)=520-100-180+28=268\]
In order to find the number of rivers polluted by only phosphate we have to exclude the regions $S\bigcap P,C\bigcap P$from the circle of P but when we do that the region of $S\bigcap P\bigcap C$ is removed twice, so we have to include the region of $S\bigcap P\bigcap C$ once. So the number of rivers polluted by only phosphate is
 \[n\left( P \right)-n\left( C\bigcap P \right)-n\left( S\bigcap P \right)+n\left( S\bigcap C\bigcap P \right)=335-180-150+28=33\]
In order to find the number of rivers polluted by only phosphate we have to exclude the regions $C\bigcap S,C\bigcap P$from the circle of C but when we do that the region of $S\bigcap P\bigcap C$ is removed twice, so we have to include the region of $S\bigcap P\bigcap C$ once. So the number of rivers polluted by only phosphate is
 \[n\left( P \right)-n\left( C\bigcap P \right)-n\left( S\bigcap P \right)+n\left( S\bigcap C\bigcap P \right)=425-100-150+28=203\]
So the number of rivers polluted by only one pollutant is $268+33+203=504$. Hence the correct option is $B$. \[\]

Note:
We can derive set expressions for the number of rivers polluted by one pollutant from $S\bigcap {{P}^{'}}\bigcap C{}^{'},{{S}^{'}}\bigcap P\bigcap C{}^{'},{{S}^{'}}\bigcap {{P}^{'}}\bigcap C$ using De-morgan’s law ${{\left( A\bigcup B \right)}^{'}}={{A}^{'}}\bigcap {{B}^{'}}$ and distributive property of union and intersection without the Venn diagram. We can also verify that $n\left( S\bigcup P\bigcup C \right)=n\left( S \right)+n\left( P \right)+n\left( S \right)-n\left( S\bigcap P \right)-n\left( P\bigcap C \right)-n\left( C\bigcap S \right)+n\left( S\bigcap P\bigcap C \right)$. The number of elements of set is also cardinality and denoted by $n\left( A \right)$ or $\left| A \right|$.