Question

In a particular section of class IX, 40 students were asked about the month of their birth and the following graph was prepared for data so obtained.

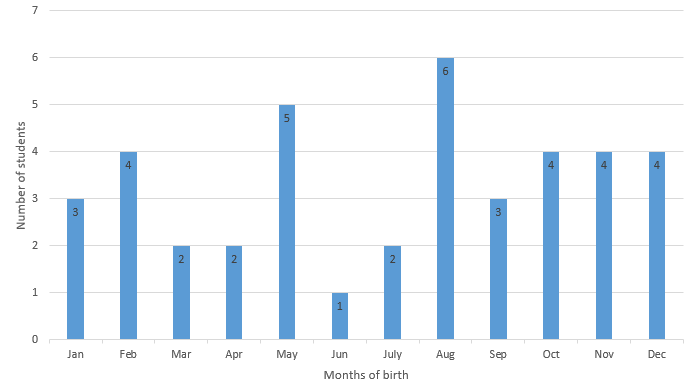
Find the probability that a student of the class was born in August.

Answer 1

Hint: To find out the probability of a desired outcome we are provided with the formulae
\[ P(A) = \dfrac{{n(E)}}{{n(S)}}\]
Where, P(A) is Probability of an event, n(E) is Number of desired outcome and n(S) is Total number of outcomes. Using this formula we can find the probability of students of class being born in August.

Complete step by step solution:
Given,
Total number of outcomes will be equal to the total number of students in the class.
i.e. n(S) = 40 (Total number of students)
Also the number of desired outcomes will be equal to the number of students who were born in August.
i.e. n(E) = 6 (Number of students who was born in august see in above bar graph)
If we let P(A) be the probability of choosing a student who was born in the month of August out of all the total students.
Then by using the formulae \[ P(A) = \dfrac{{n(E)}}{{n(S)}}\]
Substituting the values of n(E) and n(S), we will get
\[P(A) = \dfrac{6}{{40}}\]
\[ \Rightarrow P(A) = \dfrac{3}{{20}}\]
P(A) Probability of choosing a student who was born in the month of August is $\dfrac{3}{{20}}$

Note: Probability of any event will be either 0 or 1 or between 0 and 1. Zero will be the case of the probability if there are no chances of occurring of that event. One will be the probability if it is sure that a certain event is definitely going to take place. Similarly we can find the probability that a student of the class was born in a different month. We follow the same procedure as above.