Question

In a parallelogram ABCD, measure of angle D is 115 degree. Determine the measure of angle A and angle B.

Answer 1

Hint: Use the facts that the opposite angles of a parallelogram are equal and the sum of the adjacent angles is 180 degrees.

Complete step-by-step answer:

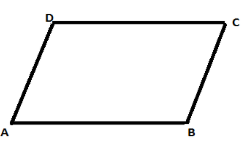
We know that the parallelogram is a quadrilateral with two pairs of parallel sides. The opposite sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure.

The measure of angle D is given to us. That is:
$\angle D={{115}^{\circ }}$
We need to find out the measure of angle B and angle A.
As we can see that angle B is the opposite angle of angle D,
$\angle B=\angle D={{115}^{\circ }}$
Sum of the adjacent angles of a parallelogram is 180 degrees.
Here the adjacent angle of B is angle A. Therefore,
$\angle B+\angle A={{180}^{\circ }}$
$\Rightarrow {{115}^{\circ }}+\angle A={{180}^{\circ }}$
$\Rightarrow \angle A={{180}^{\circ }}-{{115}^{\circ }}={{65}^{\circ }}$
Therefore,
$\angle A={{65}^{\circ }},\angle B={{115}^{\circ }}$
Measure of angle A is 65 degree and the measure of angle B is 115 degree.

Note: Alternatively, at first we can find out the measure of angle C, by using the fact that the sum of adjacent angles of a parallelogram is 180 degrees. Then find out the measure of angle A, as angle A is the opposite angle of angle C.