Question

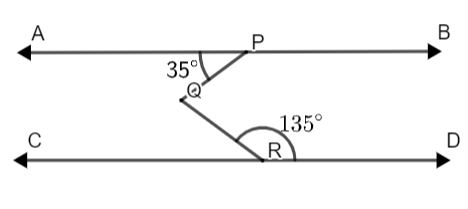
In a figure $\left. AB \right\|CD$, $\angle APQ={{35}^{\circ }}$ and $\angle QRD={{135}^{\circ }}$ find $\angle PQR$.

Answer 1

Hint: Find the angle $\angle PQF$using the angle $\angle APQ$. Then find the angle \[\angle FQR\] using the angle $\angle QRD$. Since angle $\angle PQR$ is the sum of the angle $\angle PQF$ and the angle \[\angle FQR\], so Add both the angles to get the required angle $\angle PQR$.

Complete step by step solution:

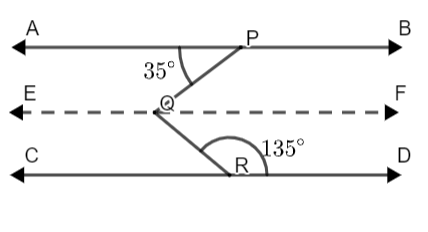
$\overleftrightarrow{EF}$is drawn, which is passing through ‘Q’ and parallel to both $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$.
As we know $\overleftrightarrow{AB}$ is parallel to $\overleftrightarrow{EF}$ and $\angle APQ={{35}^{\circ }}$
So, $\angle PQF={{35}^{\circ }}$ (as alternate interior angles are same)
Again we know $\overleftrightarrow{EF}$ is parallel to $\overleftrightarrow{CD}$ and $\angle QRD={{135}^{\circ }}$
So, \[\angle FQR+\angle QRD={{180}^{\circ }}\] (as the sum of consecutive interior angles$={{180}^{\circ }}$)
\[\begin{align}
  & \Rightarrow \angle FQR+{{135}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle FQR={{180}^{\circ }}-{{135}^{\circ }} \\
 & \Rightarrow \angle FQR={{45}^{\circ }} \\
\end{align}\]
Now, from the above figure we can conclude that
$\begin{align}
  & \angle PQR=\angle PQF+\angle FQR \\
 & \Rightarrow \angle PQR={{35}^{\circ }}+{{45}^{\circ }} \\
 & \Rightarrow \angle PQR={{80}^{\circ }} \\
\end{align}$
This is the required solution of the given question.

Note: There are some pairs of angles in the above figure.
Angle $\angle APQ$ and angle $\angle PQF$, angle $\angle QRC$ and angle \[\angle FQR\], angle$\angle BPQ$ and angle $\angle PQE$, angle $\angle EQR$ and angle $\angle QRD$ are the pairs of alternate interior angles which are same.
Similarly, angle $\angle APQ$ and angle $\angle PQE$, angle $\angle BPQ$ and angle $\angle PQE$, angle $\angle EQR$ and angle $\angle QRC$, angle \[\angle FQR\] and angle $\angle QRD$ are the pairs of consecutive interior angles whose sum is$={{180}^{\circ }}$.