Question

In a $\Delta PQR$ Let $\angle PQR={{30}^{\circ }}$ and the sides PQ and QR have length $10\sqrt{3}\text{ and 10}$ respectively, then which of the following statement is/are true? This question has multiple options correct.
\[\begin{align}
  & \text{A}.\angle QPR={{45}^{\circ }} \\
 & \text{B}.\text{ The area of triangle PQR is 25}\sqrt{3}\text{ and }\angle \text{QRP=12}{{\text{0}}^{\circ }} \\
 & \text{C}.\text{ The radius of the in circle of the triangle PQR is 10}\sqrt{3}-15 \\
 & \text{D}.\text{ The area of circumcircle of the triangle PQR is 100}\pi \\
\end{align}\]

Answer 1

Hint: To solve this question, we will first calculate length of side PR using formula $\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$ where ABC is a triangle as given below:

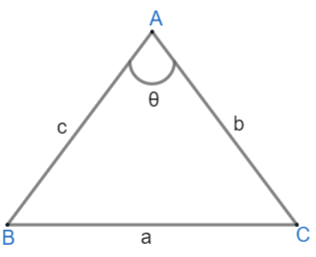
Side length AB = c, BC = a and AC = b. Also, $\angle BAC=\theta $
After this, we will calculate area of triangle formed by using formula:
\[\text{Area}=\dfrac{1}{2}\times cb\sin \theta \]
Where ABC triangle is as above.
After this we will solve option C and option D by using the formula of radius of incircle and radius of circumcircle of triangle, it is given as \[\text{radius of incircle of }\Delta =\dfrac{\text{area of }\Delta }{S}\] where \[S=\dfrac{a+b+c}{2}\] in $\Delta ABC$ above and \[\text{radius of circumcircle}=\dfrac{a}{\sin 2\theta }\] where $\angle BAC=\theta \text{ and a}=BC$ in above $\Delta ABC$

Complete step by step answer:
Consider the triangle given as PQR below:

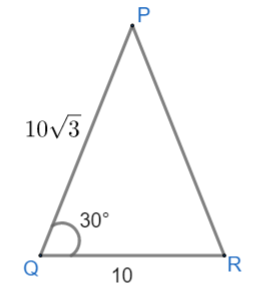
Given $\angle PQR={{30}^{\circ }}$, QR = 10 and $PQ=10\sqrt{3}$
First of all we will calculate the value of length PR for that we will use $\cos \theta $ which is given by:

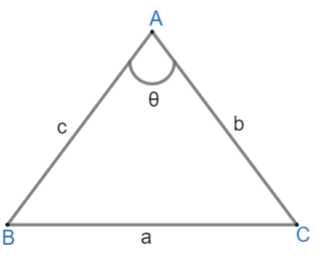
If $\Delta ABC$ is there and angle $\angle A=\theta $ then $\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
We will use this formula to calculate length PR of $\Delta PQR$
We have $PQ=10\sqrt{3}$ let it be b of above equation.
 QR = 10 let it be c of above equation and $\theta ={{30}^{\circ }}$
Then, using formula we have,
\[\begin{align}
  & \cos {{30}^{\circ }}=\dfrac{{{\left( 10\sqrt{3} \right)}^{2}}+{{\left( 10 \right)}^{2}}-{{\left( PR \right)}^{2}}}{2\times 10\times 10\sqrt{3}} \\
 & \cos {{30}^{\circ }}=\dfrac{300+100-{{\left( PR \right)}^{2}}}{200\sqrt{3}} \\
\end{align}\]
We have the value of $\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}$ Using this in above we get:
\[\dfrac{\sqrt{3}}{2}=\dfrac{400-{{\left( PR \right)}^{2}}}{200\sqrt{3}}\]
Calculating 2 from denominator of both sides we get:
\[\sqrt{3}=\dfrac{400-{{\left( PR \right)}^{2}}}{100\sqrt{3}}\]
Cross multiply above equation:
\[\begin{align}
  & 100\times 3=400-{{\left( PR \right)}^{2}} \\
 & 300-400=-{{\left( PR \right)}^{2}} \\
 & -100=-{{\left( PR \right)}^{2}} \\
 & {{\left( PR \right)}^{2}}=100 \\
\end{align}\]
Taking square root both sides we get PR = 10
Now, we have PR = QR = 10 in $\Delta PQR$
We have a theorem as "equal side of a triangle correspond to equal angle".
Using this in $\Delta PQR$ we have:

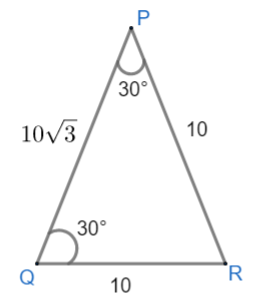
$\angle QPR={{30}^{\circ }}$ as QR = 10 was corresponding side of \[\angle QPR\] and PR = 10 is corresponding side of $\angle PQR={{30}^{\circ }}$
Hence, we have $\angle QPR={{30}^{\circ }}$
Now, we will use angle sum property of triangle to calculate the third angle $\angle PRQ$ of $\Delta PQR$
Angle sum property states that sum of all angles of a triangle is ${{180}^{\circ }}$
So, in $\Delta PQR$ we have:
\[\angle PQR+\angle QPR+\angle PRQ={{180}^{\circ }}\]
Using $\angle PQR=\angle QPR={{30}^{\circ }}$
\[\begin{align}
  & {{30}^{\circ }}+{{30}^{\circ }}+\angle PRQ={{180}^{\circ }} \\
 & \angle PRQ={{180}^{\circ }}-{{60}^{\circ }} \\
 & \angle PRQ={{120}^{\circ }} \\
\end{align}\]
Here, finally we have \[\angle PRQ={{120}^{\circ }}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)}\]
Now, we will calculate area of $\Delta PQR$
Let $\Delta ABC$ be given and $\angle C$ is given as $\theta $ as shown below:

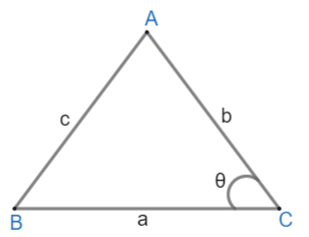
Let AB = c, BC = a and AC = b then \[\text{area of }\Delta \text{ABC}=\dfrac{1}{2}ab\sin \theta \]
Comparing this scenario with our $\Delta PQR$ we have that $\angle QPR={{30}^{\circ }},PQ=10\sqrt{3}\text{ and }PR=10$
Using the formula of area of triangle stated above in $\Delta PQR$ we have:
\[\begin{align}
  & \text{Area of }\Delta PQR=\dfrac{1}{2}\times PQ\times PR\times \sin {{30}^{\circ }} \\
 & \text{Area of }\Delta PQR=\dfrac{1}{2}\times 10\sqrt{3}\times 10\times \sin {{30}^{\circ }} \\
\end{align}\]
Value of $\sin {{30}^{\circ }}=\dfrac{1}{2}$
\[\begin{align}
  & \text{Area of }\Delta PQR=\dfrac{1}{2}\times 10\sqrt{3}\times 10\times \dfrac{1}{2} \\
 & \text{Area of }\Delta PQR=5\times 5\sqrt{3} \\
 & \text{Area of }\Delta PQR=25\sqrt{3}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)} \\
\end{align}\]
Now, we have to calculate the value of radius of incircle formed in $\Delta PQR$

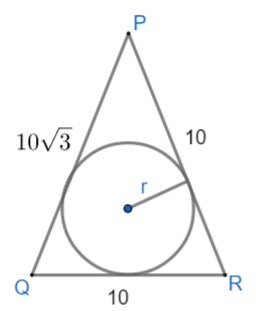
Incircle is a circle formed inside a triangle with circumference touching the sides of the triangle.
Let r be the radius of incircle.
We have \[\text{radius of incircle of }\Delta =\dfrac{\text{area of }\Delta }{S}\]
Where \[S=\dfrac{a+b+c}{2}\]

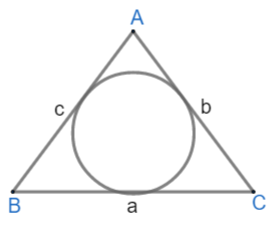
Where ABC is the triangle and AB = c, BC = a and AC = b.
Using this formula of radius of incircle of a triangle in $\Delta PQR$ we get:
\[\text{Radius r}=\dfrac{\text{area of }\Delta PQR}{S}\]
We have here,
\[\begin{align}
  & S=\dfrac{PQ+PR+QR}{2} \\
 & S=\dfrac{10+10+10\sqrt{3}}{2} \\
 & S=\dfrac{20+10\sqrt{3}}{2} \\
\end{align}\]
Also from equation (ii) we have area of $\Delta PQR=25\sqrt{3}$ using this in radius r we get:
\[\begin{align}
  & r=\dfrac{\dfrac{25\sqrt{3}}{20+10\sqrt{3}}}{2} \\
 & r=\dfrac{25\sqrt{3}}{10+5\sqrt{3}} \\
\end{align}\]
Now, we will rationalize the obtained term by multiplying and dividing by $10-5\sqrt{3}$
We get, \[r=\dfrac{25\sqrt{3}\left( 10-5\sqrt{3} \right)}{\left( 10+5\sqrt{3} \right)\left( 10-5\sqrt{3} \right)}\]
We have formula $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$
Using this in above we get,
\[\begin{align}
  & r=\dfrac{\left( 25\sqrt{3} \right)\left( 10-5\sqrt{3} \right)}{100-{{\left( 5\sqrt{3} \right)}^{2}}} \\
 & r=\dfrac{250\sqrt{3}-25\times 5\times 3}{100-25\times 3} \\
 & r=\dfrac{250\sqrt{3}-375}{25} \\
\end{align}\]
Taking 25 common:
\[\begin{align}
  & r=\dfrac{25\left( 10\sqrt{3}-15 \right)}{25} \\
 & r=10\sqrt{3}-15 \\
\end{align}\]
So, value of \[\text{Radius of incircle of}\Delta PQR=10\sqrt{3}-15\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iii)}\]
Now, finally we will calculate the area of the circumcircle of triangle PQR.
Circumcircle of a triangle is a circle which passes through all corner points of a triangle.

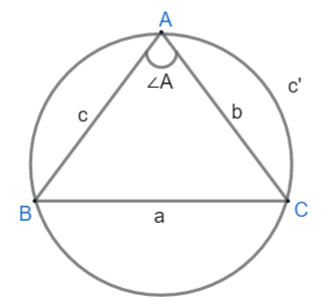
Here AB = c, BC = a and AC = b.
ABC is a triangle and c' is the circumcircle.
We have a formula of calculating radius of circumcircle.
We have \[\text{Radius of circumcircle of }\Delta ABC=\dfrac{a}{2\sin A}\]
Now, we will use this formula of radius in $\Delta PQR$
Let radius of circumcircle $\Delta PQR$ be R.
Then, \[\begin{align}
  & R=\dfrac{QR}{2\left( \angle QPR \right)} \\
 & R=\dfrac{10}{2\sin {{30}^{\circ }}} \\
\end{align}\]
We have $\sin {{30}^{\circ }}=\dfrac{1}{2}$
\[R=\dfrac{10}{2\times \dfrac{1}{2}}=10\]
So, we have the radius of circumcircle of $\Delta PQR$ is R = 10.
Area of the circle formula is $\pi {{r}^{2}}$ where r is the radius of the circle.
Here, R = 10 in triangle PQR circumcircle.
So, \[\begin{align}
  & \text{Area of circumcircle of }\Delta PQR=\pi {{\left( R \right)}^{2}} \\
 & \Rightarrow \pi {{\left( 10 \right)}^{2}} \\
 & \Rightarrow 100\pi \text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iv)} \\
\end{align}\]

Now from equation (ii), (iii) and (iv) we see that option B, C and D are correct and option A is wrong.

Note: A possibility of confusion for students can be at the point where we are calculating the value of radius of circumcircle of $\Delta PQR$. Where we have considered side QR instead of side PQ and PR. We can also go for selecting PQ or PR for the purpose, the answer would be the same in any case.
If $PQ=10\sqrt{3}$ is selected then
\[\begin{align}
  & \text{Radius of circumcircle of }\Delta PQR=\dfrac{PQ}{2\sin \left( PRQ \right)} \\
 & R=\dfrac{10\sqrt{3}}{2\sin {{120}^{\circ }}} \\
\end{align}\]
We have $\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}$
\[R=\dfrac{10\sqrt{3}}{2\times \dfrac{\sqrt{3}}{2}}=10\]
So, radius R is anyway the same.