Question

In a compound microscope the focal length of the objective is 0.5 cm and the focal length of eyepiece is 5 cm. The real image of the object is formed at a distance of 15.5 cm from the objective. If the final image is formed at a distance of 25 cm from the eyepiece, what is the magnifying power of the microscope?
A. 180
B. 0.2
C. 20
D. 150

Answer 1

Hint: A compound microscope is an optical device which is used for the purpose of obtaining enlarged images of tiny objects. It uses a system of two convex lenses (objective and eyepiece) to create a magnified image.

Formula used:
Magnification produced by a compound lens is given as:
$m = \dfrac{v_o}{u_o} \left( 1 + \dfrac{25 cm}{f_e} \right) $
where subscripts o and e are used to denote objective and eyepiece respectively.
For a spherical lens:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where symbols have their usual meaning.

Complete step by step answer:
Here is a rough diagram of the situation given to us:

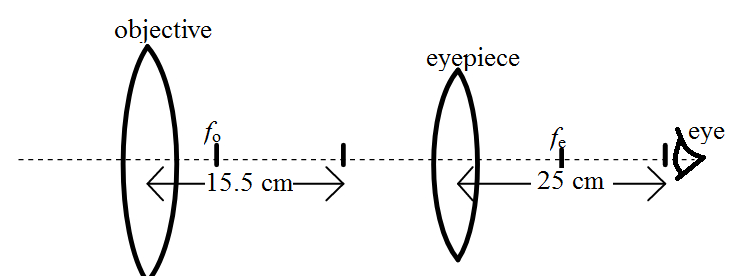
Magnification for a compound lens is the product of linear magnification of objective and angular magnification of eyepiece:
$m = m_o \times m_e$.
We know that linear magnification for a convex lens can be written as the ratio of object and image distances. So, we will have to find the object distance for the objective. We proceed as follows;
Given that $f_o $ = 0.5 cm and $v_o$ = 15.5 cm,
$\dfrac{1}{u} = \dfrac{1}{v} - \dfrac{1}{f}$
$\implies u = \dfrac{vf}{ f - v} = \dfrac{15.5 \times 0.5 }{0.5 – 15.5 } = \dfrac{15.5}{30}$cm.

Therefore, the linear magnification can now be written as:
$m_o = \dfrac{v}{u } = \dfrac{15.5}{(15.5/30)}$= 30.

The angular magnification for the eyepiece is written as:
$m_e = 1+ \dfrac{25 cm}{f_e} =1+ \dfrac{25 cm}{5 cm} $= 6.

The product of the two magnifications will give us the magnification of the compound microscope as:

$m = 30 \times 6 = 180$

Therefore, the correct answer is option (A).

Note:
Because of sign conventions, we use the focal length of the convex lens to be positive and so will be the image distance. The final image is created on the retina of the observer which is necessarily kept at least 25 cm away to clearly observe something. The real image of the object still forms at some distance from the eyepiece.