Question

In a compound AB, the ionic radii of ${A^ + }$ and ${B^ - }$ are $88\,\,pm$ and $200\,\,pm$ respectively the coordination number of ${A^ + }$ is:
(A) $6$
(B) $8$
(C) $4$
(D) $12$

Answer 1

Hint: To solve this question, we must first understand how we can determine the Coordination number by using the ionic radii or radius ratio. Then we need to assess the concepts and use the correct formula to evaluate the coordination number and then only we can conclude the correct answer.

Complete step-by-step solution:Before we move forward with the solution of this given question, let us first understand some basic concepts about the radius ratio rule:
Radius Ratio refers to the ratio of smaller ionic radius (cation) by the ratio of larger ionic radius (anion). Hence, Radius ratio:
 \[\rho {\text{ }} = \,\,{r_{cation}}/{r_{anion}}\] .
This rule helps in the determination of arrangement of ions in various types of crystal structures.
It also helps to determine the stability of an ionic crystal structure. For instance, larger cations will fill the larger voids like cubic sites whereas smaller cations will fill the smaller voids such as tetrahedral sites.
The different ranges of Radius Ratio results in different coordination number and coordination as follows:

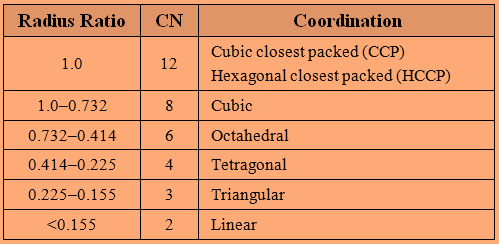
Now, let’s find the radius ratio for the given entity:
$\rho = \,\,\dfrac{{{r^ + }}}{{{r^ - }}}\,\, = \,\,\dfrac{{88}}{{200}}\,\, = $ $0.44$
So, the radius ratio is $0.44$ and it lies in the range of $0.732 - 0.414$ .
Therefore, the coordination number of ${A^ + }$ is $6$ .

So, clearly we can conclude that the correct answer is Option (A).

Note:The electrostatic interaction between charged spheres is responsible for the formation of bonding in an ionic model. The determination of the sizes of the ionic radius is possible by the internuclear separation of the separate contributions of the anion from cation.