Question

In a complex plane, what is the relation between the points $1 + 3i,5 + i,3 + 2i$?
${\text{A}}{\text{. }}$Vertices of a right angled triangle
${\text{B}}{\text{. }}$Collinear
${\text{C}}{\text{. }}$Vertices of an equilateral triangle
${\text{D}}{\text{. }}$Vertices of an obtuse angled triangle

Answer 1

Hint- Here, we will proceed by comparing the position vectors of the given points with $a + ib$ in order to find the real and imaginary part of the points and then we will use the distance formula i.e., $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $ to find the distance between all the three points.

Complete step-by-step answer:

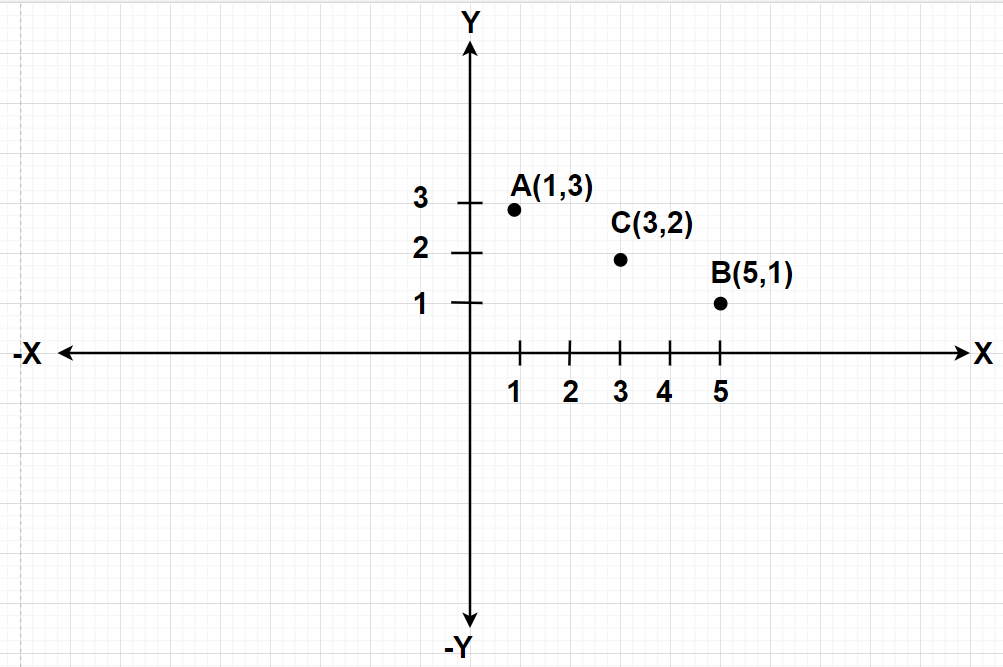
Given points in the complex plane are $1 + 3i,5 + i,3 + 2i$.
Let these points are represented as A, B and C respectively such that the position vector of point A is $1 + 3i$, the position vector of point B is $5 + i$ and the position vector of C is $3 + 2i$.
As we know that the position vector of any point X(a,b) in the complex plane is given by $a + ib$
So, the coordinates of point A is (1,3), the coordinates of point B is (5,1) and the coordinates of point C is (3,2).
According to the distance formula, the distance between any two points ${\text{A}}\left( {{x_1},{y_1}} \right)$ and ${\text{B}}\left( {{x_2},{y_2}} \right)$ is given by $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} {\text{ }} \to {\text{(1)}}$
Using the formula given by equation (1),
Distance between two points A(1,3) and B(5,1), $
  {\text{AB}} = \sqrt {{{\left( {5 - 1} \right)}^2} + {{\left( {1 - 3} \right)}^2}} \\
   \Rightarrow {\text{AB}} = \sqrt {{{\left( 4 \right)}^2} + {{\left( { - 2} \right)}^2}} \\
   \Rightarrow {\text{AB}} = \sqrt {16 + 4} \\
   \Rightarrow {\text{AB}} = \sqrt {20} \\
   \Rightarrow {\text{AB}} = 2\sqrt 5 \\
 $
Distance between two points B(5,1) and C(3,2), \[
  {\text{BC}} = \sqrt {{{\left( {3 - 5} \right)}^2} + {{\left( {2 - 1} \right)}^2}} \\
   \Rightarrow {\text{BC}} = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( 1 \right)}^2}} \\
   \Rightarrow {\text{BC}} = \sqrt {4 + 1} \\
   \Rightarrow {\text{BC}} = \sqrt 5 \\
 \]
Distance between two points A(1,3) and C(3,2), \[
  {\text{AC}} = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( {2 - 3} \right)}^2}} \\
   \Rightarrow {\text{AC}} = \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} \\
   \Rightarrow {\text{AC}} = \sqrt {4 + 1} \\
   \Rightarrow {\text{AC}} = \sqrt 5 \\
 \]
Clearly, we can see that AB is equal to the sum of BC and AC i.e., AB=BC+AC
Therefore, all the points A, B and C lie on the same straight line where point C is the midpoint of the line AB. So, the points $1 + 3i,5 + i,3 + 2i$ in the given complex plane are collinear.
Hence, option B is correct.

Note- In this particular problem, the point with position $1 + 3i$ have 1 as the real part and 3 as the imaginary point, the point with position $5 + i$ have 5 as the real part and 1 as the imaginary point and the point with position $3 + 2i$ have 3 as the real part and 2 as the imaginary point. The real part and the imaginary part in the position vector of the points represents the x-coordinate and y-coordinate of that point respectively.