Question

If \[y = x{e^{ - x}}\], what are the points of inflection of the graph \[f(x)\]?

Answer 1

Hint: Here, we will learn some new concepts like concavity, points of inflection of functions and so on. To find the points of inflection, first we need to find a second derivative of this function. If the first derivative and the second derivative of this functions exist and continuous, the,
The inflection point is \['a'\] for which \[f''(a) = 0{\text{ or undefined}}\]
We will solve the problem by using some derivative formulas like \[\dfrac{d}{{dx}}{e^x} = {e^x}\] and \[\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}\]
And also, we will use the product rule which is \[\dfrac{d}{{dx}}uv = u\dfrac{d}{{dx}}v + v\dfrac{d}{{dx}}u\] where \[u{\text{ and }}v\] are functions in \[x\].

Complete step by step answer:
Inflection points are the points at which the graph changes its concavity. Concavity means the concave or convex nature of a graph. It also defines the concave-up or concave-down nature of graphs.
Suppose that there is a function \[y = f(x)\].
If the first derivative and the second derivative of this functions exist and continuous, the,
The inflection point is \['a'\] for which \[f''(a) = 0{\text{ or undefined}}\]
So, in the question, the given function is \[y = x{e^{ - x}}\]
To find the points of inflection, first we need to find a second derivative of this function.
Let us first find the first derivative.
\[y' = \dfrac{d}{{dx}}x{e^{ - x}}\]
By applying product rule, (as there are two functions as a single term)
\[ \Rightarrow y' = x\dfrac{d}{{dx}}{e^{ - x}} + {e^{ - x}}\dfrac{d}{{dx}}x\]
\[ \Rightarrow y' = x( - {e^{ - x}}) + {e^{ - x}}\]
So, we get the first derivative as,
\[ \Rightarrow y' = {e^{ - x}}(1 - x)\]
Now, let us find the second derivative.
\[y'' = \dfrac{d}{{dx}}{e^{ - x}}(1 - x)\]
\[ \Rightarrow y'' = {e^{ - x}}\dfrac{d}{{dx}}(1 - x) + (1 - x)\dfrac{d}{{dx}}{e^{ - x}}\]
Now, on simplification, we get,
\[ \Rightarrow y'' = - {e^{ - x}} + (1 - x)( - {e^{ - x}})\]
\[ \Rightarrow y'' = {e^{ - x}}(x - 2)\]
Now, to get points of inflection, equate the second derivative to zero.
\[ \Rightarrow y'' = {e^{ - x}}(x - 2) = 0\]
So, on solving, we get \[x = 2\]
So, the point of inflection is \[x = 2\].
At this point the graph changes its concavity.

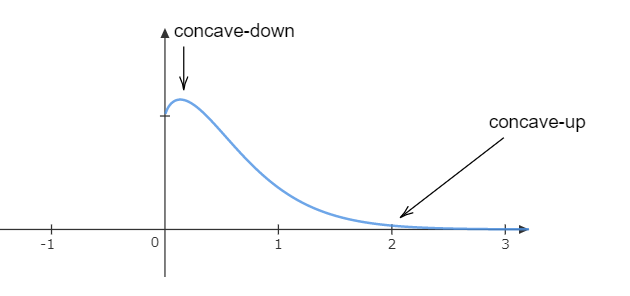
This is the graph for \[y = x{e^{ - x}}\].

Note:
In geometry and calculus, the point of inflection is also called inflection point or flex or inflection.
If the function is a decreasing function, then the point of inflection is called A falling point of inflection.
If the function is an increasing function, then the point of inflection is called A rising point of inflection.