Question

If \[X\] and \[Y\] are two nonempty sets, where \[f:X\to Y\] is function is defined such that \[f(c)=\{f(x):x\in C\}\] for \[C\subseteq X\] and \[{{f}^{-1}}(D)=\{x:f(x)\in D\}\] for \[D\subseteq Y\] , for any \[A\subseteq Y\] and \[B\subseteq Y\] then,
A). \[{{f}^{-1}}\{f(A)\}=A\]
B). \[{{f}^{-1}}\{f(A)\}=\text{A only if f(X)=Y}\]
C). \[\text{f }\!\!\{\!\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\!\!\}\!\!\text{ =B only if B}\subseteq \text{f(x)}\]
D). \[\text{f }\!\!\{\!\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\!\!\}\!\!\text{ =B }\]

Answer 1

Hint: First of all we will define \[f\] and \[{{f}^{-1}}\] in the two nonempty sets that is \[X\] and \[Y\] then by the figure \[(1)\] we can determine that we cannot define \[f(A)\] and \[f(B)\] so we will define \[{{f}^{-1}}(A)\] and \[{{f}^{-1}}(B)\] after this check all the options to find which one is correct among them.

Complete step-by-step solution:
In mathematics the word set was first of all used by a German Mathematician George Cantor. He defined the set as follows: a set is any collection into a whole of definite and distinct objects of our intuition or thought.
The objects belonging to the set are called elements or members of the set.
A set containing no element is called the empty set. It is denoted by the symbol \[\phi \]
If \[X\] and \[Y\] are two nonempty sets
Here \[f\] is defined as:
\[\Rightarrow f:X\to Y\]
Therefore the inverse of \[f\] will be defined as:
\[\Rightarrow {{f}^{-1}}:Y\to X\]

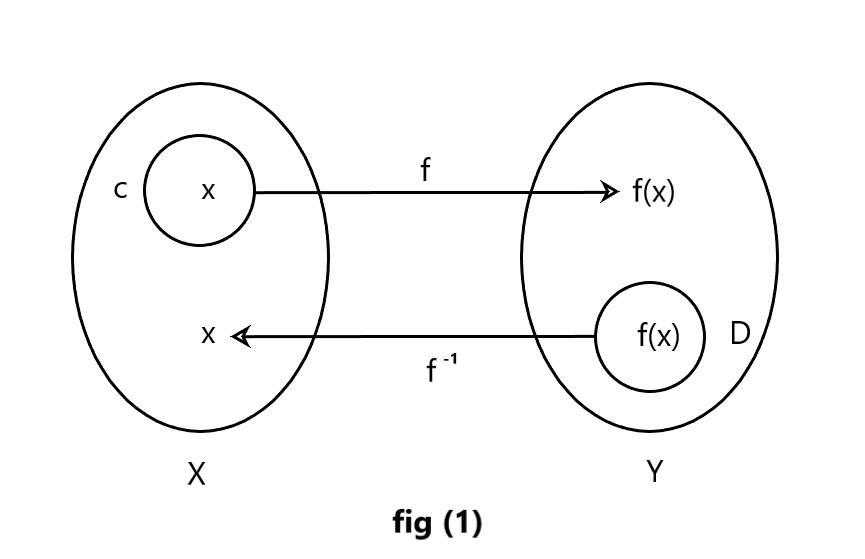
In the given figure \[(1)\] we have given two sets \[X\] and \[Y\] and define \[f\] from \[X\] to \[Y\]
Take a set inside set \[X\] and name it \[C\] such that \[C\subseteq X\] . Then take any value inside set \[C\] name it \[x\] such that image of \[x\] comes in set \[Y\] name it \[f(x)\]
If we define the inverse of these two sets in figure \[(1)\] . Take a set inside set \[Y\] name it \[D\] and take any element inside the set \[D\] and name it \[f(x)\] such that image of \[f(x)\] comes in set \[X\] name it \[x\] and the image is defined as \[{{f}^{-1}}\]
We have given that \[A\subseteq Y\] and \[B\subseteq Y\]
Hence we cannot define \[f(A)\] and \[f(B)\] so we will define \[{{f}^{-1}}(A)\] and \[{{f}^{-1}}(B)\]
Now we will check the given options:
In option \[(1)\] \[{{f}^{-1}}\{f(A)\}=A\] , \[f(A)\] is defined hence this option is incorrect.
In option \[(2)\] \[{{f}^{-1}}\{f(A)\}=\text{A only if f(X)=Y}\] , \[f(A)\] is defined hence this option is also incorrect.
In option \[(3)\] \[\text{f }\!\!\{\!\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\!\!\}\!\!\text{ =B only if B}\subseteq \text{f(x)}\]
\[\text{f }\!\!\{\!\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\!\!\}\!\!\text{ =B }\]
                    

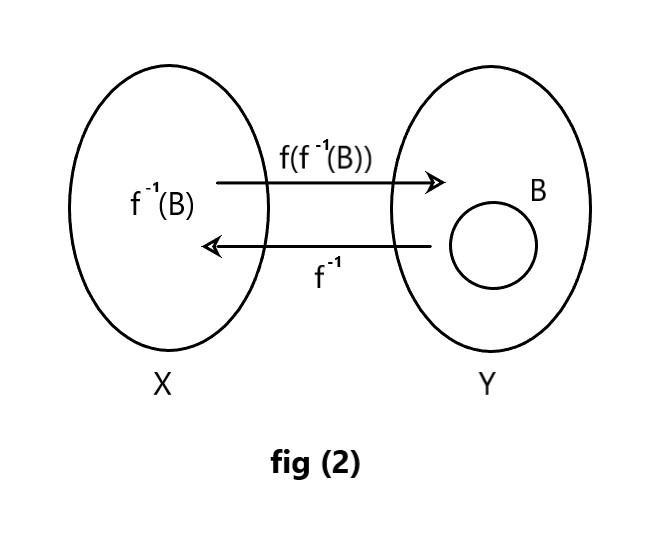
In figure \[(2)\] you can see that you have given two sets \[X\] and \[Y\] let us take a set inside set \[Y\] name it \[B\] if we define \[{{f}^{-1}}\] from \[\text{B }\]and the image will be \[{{\text{f}}^{\text{-1}}}\text{(B)}\] if we again define \[{{\text{f}}^{\text{-1}}}\text{(B)}\] through \[\text{f}\] then the image will be defined as \[\text{ }\!\!\{\!\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\!\!\}\!\!\text{ }\] and will belong to set \[\text{B }\]
Hence option \[(3)\] is correct as \[\text{f }\!\!\{\!\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\!\!\}\!\!\text{ =B }\] and \[\text{B}\subseteq \text{f(x)}\] .

Note: If in any finite set, some elements are repeated then to find the cardinality of this set repeated elements counts only once, because repetition of elements is meaningless. For example: Let \[A=\{1,2,2,3,4,4,5\}\] then clearly \[n(A)=5\] .The number of distinct elements in a finite set is also called the order of a set.