Question

if we have a trigonometric expression as $[{{\cot }^{-1}}x]+[{{\cos }^{-1}}x]=0$ , where [ . ] denotes greatest integer function, then the complete set of values of x is
( a ) (cos1, 1]
( b ) ( cos1, - cos1)
( c ) (cot1, 1]
( d ) none of these

Answer 1

Hint: What we will do is we will first draw the graph of ${{\cos }^{-1}}x$ and ${{\cot }^{-1}}x$ using concept of greatest integer function. Then we will first see for what values of x, ${{\cos }^{-1}}x$ and ${{\cot }^{-1}}x$ is equals to zero. Then we will take intersection of set of domain of values of x for $[{{\cos }^{-1}}x]=0$ and $[{{\cot }^{-1}}x]=0$.

Complete step-by-step solution:
Before we start the question, let us see what is the greatest integer function and what are its properties.
Function y = [ x ] is called greatest integer function which means the greatest integer less than or equals to x. also, if n belongs to set of integer, then y = [ x ] = n if $n\le xFor example if we put x = -3.1 in y = [ x ], then y = - 4 and if we put x = 0.2 in y = [ x ], then y = 0.
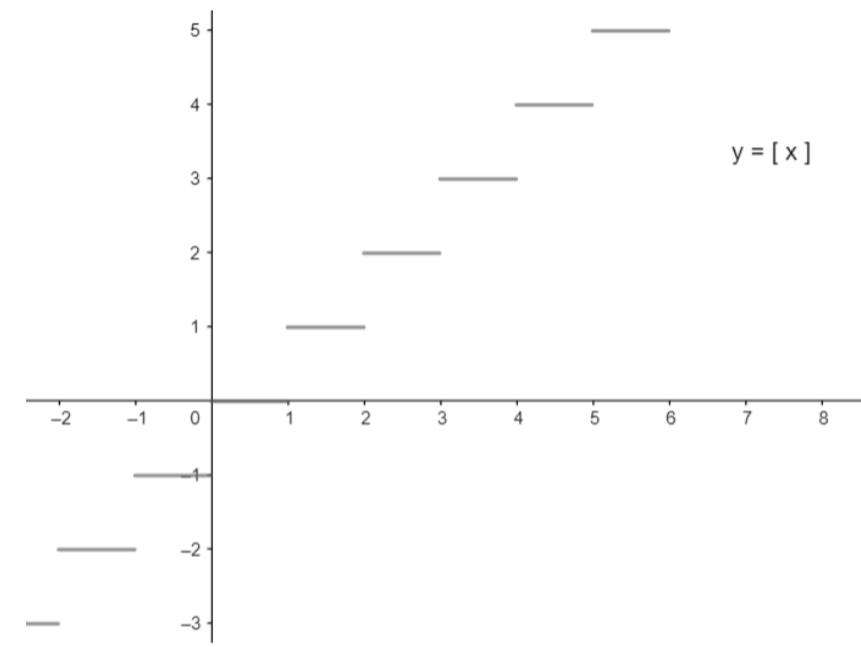
Graph of y = [ x ] is given as,

Graph of $y=[{{\cot }^{-1}}x]$ is given as,

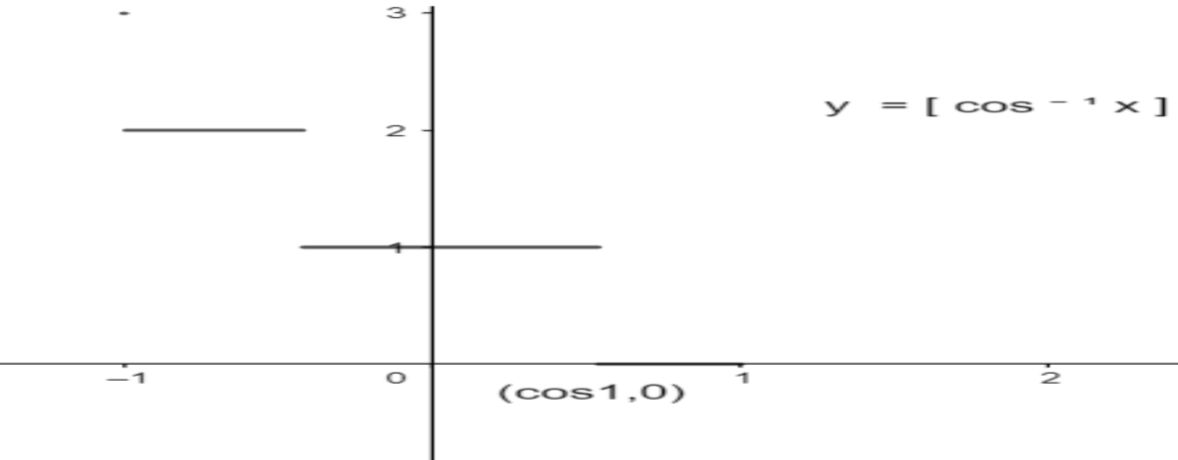
Graph of $y=[{{\cos }^{-1}}x]$ is given as

Now, in question it is given that $[{{\cot }^{-1}}x]+[{{\cos }^{-1}}x]=0$
Now, we know that range of ${{\cos }^{-1}}x$ is $0\le {{\cos }^{-1}}x\le \pi $.
So from seeing the range of ${{\cos }^{-1}}x$, we can say that ${{\cos }^{-1}}x$ is always positive for all values of x. where x belongs to a set of real numbers.
Also, we know that range of ${{\cot }^{-1}}x$ is $0<{{\cot }^{-1}}x\le \pi $.
So from seeing the range of ${{\cot }^{-1}}x$, we can say that ${{\cos }^{-1}}x$ is always positive for all values of x. where x belongs to a set of real numbers.
Now for, values of ${{\cot }^{-1}}x$ and ${{\cos }^{-1}}x$, $[{{\cot }^{-1}}x]+[{{\cos }^{-1}}x]=0$is true when both $[{{\cot }^{-1}}x]$ and $[{{\cos }^{-1}}x]$ are equals to zero.
Now, from graph of $[{{\cos }^{-1}}x]$, $[{{\cos }^{-1}}x]$ is always zero for values between cos1 and 1 that is,
$[{{\cos }^{-1}}x]=0;x\in (\cos 1,1]$….( i )
Now, from graph of $[{{\cot }^{-1}}x]$, $[{{\cot }^{-1}}x]$ is always zero for values between cot1 and $\infty $ that is,
$[{{\cot }^{-1}}x]=0;x\in (\cot 1,\infty )$……( ii )
Taking intersection of equation ( i ) and ( ii )
So, set of all values x for which $[{{\cot }^{-1}}x]+[{{\cos }^{-1}}x]=0$ is $x\in (\cot 1,1]$
Hence, option ( c ) is true.

Note: For finding domain of functions which are formed by combination of some function of x and greatest integer function, knowledge of graph is must. If we have $f(x)={{f}_{1}}(x)+{{f}_{2}}(x)$ , then domain of f(x) is equals to domain of ${{f}_{1}}(x)\cap {{f}_{2}}(x)$.