Question

If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.

Answer 1

Hint: We will start with considering two triangles which are similar to each other. And then we will calculate their areas to find the ratio of them. On the other hand using the properties of similar triangles we will reach our desired result.

Complete step-by-step answer:
We consider two similar triangles \[\Delta ABC\] and \[\Delta PQR;\]

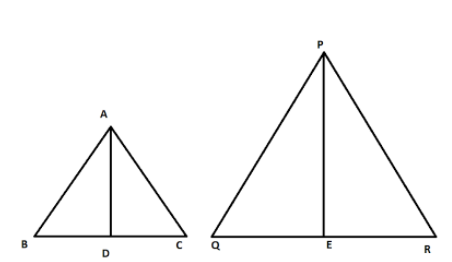
According to the stated theorem,
area of \[\Delta ABC/area\;of\;\Delta PQR\;\]\[ = \;{\left( {\dfrac{{AB}}{{PQ}}} \right)^2}\; = {\left( {\dfrac{{BC}}{{QR}}} \right)^2}\; = \;{\left( {\dfrac{{CA}}{{RP}}} \right)^2}\]
As, \[Area{\text{ }}of{\text{ }}triangle{\text{ }} = \;\;\dfrac{1}{2} \times Base{\text{ }} \times {\text{ }}Height\]
To find the area of \[\Delta ABC\] and \[\Delta PQR\] draw the altitudes AD and PE from the vertex A and P of \[\Delta ABC\] and \[\Delta PQR\], respectively, as shown in the figure given below:
Now, area of \[\Delta ABC{\text{ }} = \;\dfrac{1}{2}\; \times {\text{ }}BC{\text{ }} \times {\text{ }}AD\]
\[area\,\,of\,\Delta PQR{\text{ }} = \;\dfrac{1}{2}\; \times {\text{ }}QR{\text{ }} \times {\text{ }}PE\]
The ratio of the areas of both the triangles can now be given as:
area of\[\;\Delta ABC/area\, of \Delta PQR\;\]\[ = \;\dfrac{{\dfrac{1}{2}\; \times {\text{ }}BC{\text{ }} \times {\text{ }}AD}}{{\;\dfrac{1}{2}\; \times {\text{ }}QR{\text{ }} \times {\text{ }}PE}}\]
\[ \Rightarrow \]\[area\;of\;\Delta ABC/area\;of\;\Delta PQR\;\] \[ = \;\dfrac{{{\text{ }}BC{\text{ }} \times {\text{ }}AD}}{{\;{\text{ }}QR{\text{ }} \times {\text{ }}PE}}\]……………. (1)
Now in \[\Delta ABD\] and \[\Delta PQE\], it can be seen that:
\[\angle ABC{\text{ }} = \angle PQR{\text{ }}\left( {Since{\text{ }}\Delta ABC{\text{ }}\sim{\text{ }}\Delta PQR} \right)\]
\[\angle ADB{\text{ }} = \angle PEQ\] (Since both the angles are \[90^\circ \])
From AA criterion of similarity \[\Delta ADB{\text{ }}\sim{\text{ }}\Delta PEQ\]
\[ \Rightarrow \dfrac{{AD}}{{PE}} = \dfrac{{AB}}{{PQ}}\] …………….(2)
Since it is known that ΔABC~ ΔPQR,
\[\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AC}}{{PR}}\] …………….(3)
Substituting this value in equation (1), we get
area of \[\Delta ABC/area\;of\;\Delta PQR\;\] \[ = \dfrac{{AB}}{{PQ}} \times \dfrac{{AD}}{{PE}}\]
Using equation (2), we can write
area of \[\Delta ABC/area\;of\;\Delta PQR\;\] \[ = \dfrac{{AB}}{{PQ}} \times \dfrac{{AB}}{{PQ}}\]
⇒area of \[\Delta ABC/area\;of\;\Delta PQR\;\] \[ = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2}\]
Also from equation (3),
area of \[\Delta ABC/area\;of\;\Delta PQR\;\]\[ = \;{\left( {\dfrac{{AB}}{{PQ}}} \right)^2}\; = {\left( {\dfrac{{BC}}{{QR}}} \right)^2}\; = {\left( {\dfrac{{CA}}{{RP}}} \right)^2}\]
This proves that the ratio of the area of two similar triangles is proportional to the squares of the corresponding sides of both the triangles.

Note: Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion. In other words, similar triangles are the same shape, but not necessarily the same size.
The triangles are congruent if, in addition to this, their corresponding sides are of equal length.