Question

If $\theta$ is the polarizing angle for a medium in which the speed of light is $v$ then according to Brewster’s Law:
A. $\theta = {\sin ^{ - 1}}\left( {\dfrac{c}{v}} \right)$
B. $\theta = {\tan ^{ - 1}}\left( {\dfrac{c}{v}} \right)$
C. $\theta = {\cos ^{ - 1}}\left( {\dfrac{c}{v}} \right)$
D. $\theta = {\sin ^{ - 1}}\left( {\dfrac{v}{c}} \right)$

Answer 1

Hint: Refractive index of a medium $a$ with respect to medium $b$ is given by taking the ratio of the velocity of light in medium $b$ and the velocity of light in medium $a$.When a ray of light is incident on denser medium at a particular angle the reflected light will be linearly polarized. The tangent of this incident angle (polarizing angle) gives the refractive index. This polarizing angle is also known as Brewster’s angle.

Formula used:
$\dfrac{{{n_a}}}{{{n_b}}} = \dfrac{{{v_b}}}{{{v_a}}}$, where ${n_a}$ and ${n_b}$ are the refractive indices of medium a and b respectively ${v_a}$ denotes the velocity of light in medium a and ${v_b}$ denote the velocity of light in medium b
$\tan \theta = \dfrac{{{n_b}}}{{{n_a}}}$, ${n_b} > {n_a}$, $\theta $ is the polarizing angle and ${n_a}$ and ${n_b}$ are the refractive indices of medium a and b respectively.

Complete step by step answer:
When light strikes at a particular angle known as Brewster’s angle the reflected and refracted rays will be perpendicular to each other and also the reflected ray will be linearly polarized.

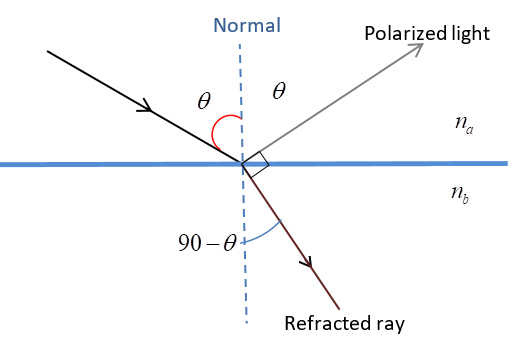
According to Brewster’s law, $\tan \theta = \dfrac{{{n_b}}}{{{n_a}}}$ here ${n_a}$ denotes the refractive index of air. Therefore ${n_a} = 1$
$\tan \theta = {n_b}$
$\theta = {\tan ^{ - 1}}{n_b}$
Similarly using ${n_a} = 1$ and speed in air as $c$ in equation $\dfrac{{{n_a}}}{{{n_b}}} = \dfrac{{{v_b}}}{{{v_a}}}$ we get
$\dfrac{1}{{{n_b}}} = \dfrac{{{v_b}}}{c}$
${n_b} = \dfrac{c}{{{v_b}}}$
Given ${v_b} = v$ and using ${n_b} = \dfrac{c}{{{v_b}}}$ in equation $\theta = {\tan ^{ - 1}}{n_b}$
$\theta = {\tan ^{ - 1}}(\dfrac{c}{v})$
The correct option is B.

Note: The incident ray will be not polarized when it hits the denser medium. It is temporarily absorbed by the medium. Electrons there oscillate in the direction of electric field vectors which are perpendicular to the refracted ray. These atoms re-emit the light to give the reflected and refracted rays. Since it is an electromagnetic wave the electric field vectors (which have the same direction in which the electrons where oscillating) will be perpendicular to the direction of propagation of the wave.
The only possible direction for the electric field vector of the reflected wave is perpendicular to the plane since it should be perpendicular to the direction of propagation of the wave .That’s the reason the reflected ray is linearly polarized. The refracted ray will be partly polarized as there are more electric field vectors in the plane than perpendicular to the plane. For all other angles than 0 degrees and Brewster angle the reflected ray also will be partly polarized.