Question

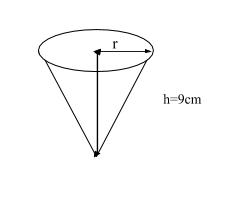
If the volume of a right circular cone of height 9cm is 48π cm3, find the diameter of its base.

Answer 1

Hint: The formula of the volume of cone can be used and the given values can be substituted to find the unknown.
 Volume of cone $ = 1/3\pi {r^2}h $
Substitute given values, so as to find the unknown.

Complete step-by-step answer:
Given : Volume of Cone $ = 48\pi $ cm3
              Height of cone = 9 cm
Let the radius of the cone be r.

We Know,
Volume of Cone $ = 1/3\pi {r^2}h $
Therefore,
 $ 1/3\pi {r^2}h $ $ = 48\pi $
Calculating for r:
 $ {r^2} = (48\pi \times 3)/(\pi h) $
Substituting the value of h:
 $ {r^2} = (48\pi \times 3)/(9\pi ) $
 $ {r^2} = 16 $
Square rooting both sides:
 $ \sqrt {{r^2}} = \sqrt {16} $
 $ r = 4 $ cm
Diameter= 2 x radius
 $ D = 2r $
 $ D = 2 \times 4 $
 $ D = 8 $ cm
Therefore, the diameter of the base of the right circular cone is 8 cm

Note: The Right circular cone has a circular base and its axis is perpendicular to the plane of the base.

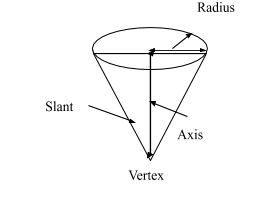
The curved surface area of a right circular cone equals the perimeter of the base times one-half slant height. The total surface area equals the curved surface area of the base.