Question

If the vectors $\hat{i}-3\hat{j}+2\hat{k},\ -\hat{i}+2\hat{j}$ represents the diagonal of a parallelogram, then its area will be
(a) $\sqrt{21}$
(b) $\dfrac{\sqrt{21}}{2}$
(c) $2\sqrt{21}$
(d) $\dfrac{\sqrt{21}}{4}$

Answer 1

Hint: Area of a parallelogram with two adjacent sides given in form, $\overrightarrow{a}$ and $\overrightarrow{b}$ is
Area of parallelogram \[=\ \left| \overrightarrow{a}\times \overrightarrow{b} \right|\]
Use the triangle law of vector addition to get the sides of the parallelogram from the given vectors of the diagonals. Law is given as when two vectors are added and represented as two sides of a triangle in the same order then the third side of the triangle gives the resultant of the other two.

Complete step-by-step answer:
We know that area of parallelogram in terms of the vectors representing their sides can be given as

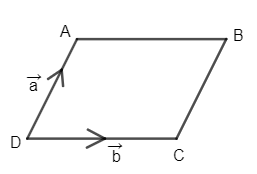
Area of parallelogram ABCD \[=\ \left| \overrightarrow{a}\times \overrightarrow{b} \right|\]
It means the area of a parallelogram is the magnitude of the cross-product of any two adjacent sides in vector form.

Here, from the given problem, we have two vectors which are representing the diagonals of parallelogram. These are given as $\left( \hat{i}-3\hat{j}+2\hat{k} \right)$ and $\left( \ -\hat{i}+2\hat{j} \right)$ . So, we can draw diagram as

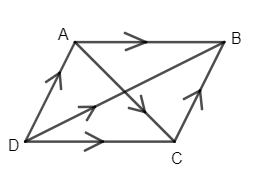
So, let we have parallelogram, whose diagonals are given as
\[\overrightarrow{\text{AC}}\ =\ \hat{i}-3\hat{j}+2\hat{k}\]
\[\overrightarrow{\text{DB}}\ =\ -\hat{i}+2\hat{j}\]

Now, we know the triangle property of addition of the vectors that when two sides of a triangle are represented by two sides of a triangle in magnitude and direction taken in the same order than the third side of that triangle represents the magnitude and direction resultant of both the vectors. So, we can get from the below triangle as

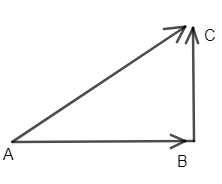
\[\overrightarrow{\text{AC}}=\ \overrightarrow{\text{AB}}+\overrightarrow{\text{BC}}\] ……………………………………………….(i)

Now, apply the triangle law of vector addition in the \[\Delta \text{BCD}\]of the parallelogram ABCD as
\[\overrightarrow{\text{DB}}=\ \overrightarrow{\text{DC}}+\overrightarrow{\text{CB}}\] ……………………………………………(ii)
Similarly, from \[\Delta \text{ACD}\], we get
\[\overrightarrow{\text{DA}}=\ \overrightarrow{\text{AC}}+\overrightarrow{\text{DC}}\]
\[\Rightarrow \overrightarrow{\text{AC}}=\ \overrightarrow{\text{DC}}-\overrightarrow{\text{DA}}\] …………………………………………(iii)

Now, we know that parallelograms have equal opposites sides and parallel to each other as well. Hence, we get
\[\overrightarrow{\text{DA}}=\ \overrightarrow{\text{CB}}\] …………………………………………………………(iv)
So, replace \[\overrightarrow{\text{DA}}\] by \[\overrightarrow{\text{CB}}\] from equation (iii). Hence, we get equation (iii) as
\[\overrightarrow{\text{AC}}=\ \overrightarrow{\text{DC}}-\overrightarrow{\text{CB}}\] ……………………………………………………..(v)

Now, add equations (ii) and (v), we get
\[\overrightarrow{\text{DB}}+\overrightarrow{\text{AC}}=\ \overrightarrow{\text{DC}}+\overrightarrow{\text{CB}}+\overrightarrow{\text{DC}}-\overrightarrow{\text{CB}}\]
\[\Rightarrow \overrightarrow{\text{DB}}+\overrightarrow{\text{AC}}=\ 2\overrightarrow{\text{DC}}\]
\[\Rightarrow \overrightarrow{\text{DC}}\ =\ \dfrac{\overrightarrow{\text{DB}}+\overrightarrow{\text{AC}}}{2}\] …………………………………………………………..(vi)

Now, subtract the equations (ii) and (v), we get
\[\overrightarrow{\text{DB}}-\overrightarrow{\text{AC}}=\ \left( \overrightarrow{\text{DC}}+\overrightarrow{\text{CB}} \right)-\left( \overrightarrow{\text{DC}}-\overrightarrow{\text{CB}} \right)\]
\[\overrightarrow{\text{DB}}-\overrightarrow{\text{AC}}=\ \overrightarrow{\text{DC}}+\overrightarrow{\text{CB}}-\overrightarrow{\text{DC}}+\overrightarrow{\text{CB}}\]
\[\overrightarrow{\text{DB}}-\overrightarrow{\text{AC}}=\ 2\overrightarrow{\text{CB}}\]
\[\Rightarrow \overrightarrow{\text{CB}}\ =\ \dfrac{\overrightarrow{\text{DB}}-\overrightarrow{\text{AC}}}{2}\] ………………………………………………………………………..(vii)

Now, put the values of \[\overrightarrow{\text{BD}}\] and \[\overrightarrow{\text{AC}}\] from the problem to the equations (vi) and (vii). Hence, we get
\[\overrightarrow{\text{DC}}\ =\ \dfrac{\hat{i}-3\hat{j}+2\hat{k}-\hat{i}+2\hat{j}}{2}\]
\[\overrightarrow{\text{DC}}\ =\ \dfrac{0-\hat{j}+2\hat{k}}{2}\,=\ \dfrac{-\hat{j}+2\hat{k}}{2}\]

Similarly, we can get value of \[\overrightarrow{\text{CB}}\] as
\[\overrightarrow{\text{CB}}\ =\ \dfrac{\left( -\hat{i}+2\hat{j} \right)-\left( \hat{i}-3\hat{j}+2\hat{k} \right)}{2}\]
\[\overrightarrow{\text{CB}}\ =\ \dfrac{-\hat{i}+2\hat{j}-\hat{i}+3\hat{j}-2\hat{k}}{2}\]
\[\overrightarrow{\text{CB}}\ =\ \dfrac{-2\hat{i}+5\hat{j}-2\hat{k}}{2}\]

Now, we can get area of parallelogram of cross-multiplying the adjacent sides \[\overrightarrow{\text{DC}}\] and \[\overrightarrow{\text{CB}}\] as given in equation (i).
We know that cross product of two vectors \[\vec{a}\ =\ {{a}_{1}}\hat{i}+{{a}_{2}}\hat{j}+{{a}_{3}}\hat{k}\] and \[\vec{b}=\ {{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k}\] is given by the relation
\[\vec{a}\times \vec{b}\ =\ \left| \begin{matrix}
   {\hat{i}} & {\hat{j}} & {\hat{k}} \\
   {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\
   {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\
\end{matrix} \right|\] ……………………………………………………(viii)

Hence, we can solve the above determinant and hence get \[\vec{a}\times \vec{b}\].
So, we can get area of parallelogram by the relation: -
Area of parallelogram ABCD \[=\ \left| \overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}} \right|\]
And we can get cross product \[\overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}}\] by the relation (viii). So, we have
\[\overrightarrow{\text{DC}}\ =\ \dfrac{-\hat{j}+2\hat{k}}{2}\,=\ \dfrac{-\hat{j}}{2}+\hat{k}\]
\[\overrightarrow{\text{CB}}\ =\ \dfrac{-2\hat{i}+5\hat{j}-2\hat{k}}{2}\ =\ -\hat{i}+\dfrac{5}{2}\hat{j}-\hat{k}\ \]

Hence, we get
\[\overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}}\ =\ \left| \begin{matrix}
   {\hat{i}} & {\hat{j}} & {\hat{k}} \\
   0 & \dfrac{-1}{2} & 1 \\
   -1 & \dfrac{5}{2} & -1 \\
\end{matrix} \right|\]

On expanding the above determinant along row 1; we get;
\[\overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}}\ =\ \hat{i}\left( \dfrac{1}{2}-\dfrac{5}{2} \right)-\hat{j}\left( 0+1 \right)+\hat{k}\left( 0-\dfrac{1}{2} \right)\]
\[\overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}}\ =\ -2\hat{i}-\hat{j}-\dfrac{{\hat{k}}}{2}\]
Now, we can calculate the magnitude of the vector \[\overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}}\].
So, we know magnitude of vector \[\left( x\hat{i}+y\hat{j}+z\hat{k} \right)\] is given as
Magnitude \[=\ \sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\]

Hence, magnitude of the vector \[\overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}}\] can be given as
\[\left| \overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}} \right|\ =\ \sqrt{{{\left( -2 \right)}^{2}}+{{\left( -1 \right)}^{2}}+{{\left( \dfrac{-1}{2} \right)}^{2}}}\]
\[=\ \sqrt{4+1+\dfrac{1}{4}}\]
\[=\ \sqrt{\dfrac{21}{4}\ }\ =\ \dfrac{\sqrt{21}}{2}\]
So, we get \[\left| \overrightarrow{\text{DC}}\times \overrightarrow{\text{CB}} \right|=\ \dfrac{\sqrt{21}}{2}\]
So, the area of parallelogram is \[\dfrac{\sqrt{21}}{2}\].
Hence, option (b) is correct.

Note: One may go wrong if he/she calculates the area of the parallelogram by calculating the cross-product of the given vectors in the problem. As the given vectors are not representing the sides of the parallelogram, they are representing the diagonals. So, we can not put them in identity \[\left| \vec{a}\times \vec{b} \right|\]. Hence, take care of it for these kinds of questions. Apply the triangle law of addition of two vectors very carefully to find the sides of the given parallelogram. Don’t confuse it with the law.
Another approach for the question would be that we can find the angles between the diagonals. And apply the formula of area of triangles with two given sides and angle between the i.e. $\dfrac{1}{2}\times a\times b\times \sin \theta $. So, find the area of parallelogram by adding the area of four triangles formed by the diagonals from the above-mentioned identity.