Question

If the vectors $4i+7j+8k$, $2i+7j+7k$ and $3i+5j+7k$ are the position vectors of the vertices $A$ , $B$ and $C$ respectively of triangle $ABC$ . The position vector of the point where the bisector of angle $A$ meets $BC$ .
(A) $3.6i+5.4j+7.2k$
(B) $2.477i+6.044j+7k$
(C) $2i+7j+8k$
(D) None of these

Answer 1

Hint: Here in this question we have been asked to find the position vector of the point where the bisector of angle $A$ meets $BC$ . When the position vectors of the vertices $A$ , $B$ and $C$ of triangle are given as $4i+7j+8k$, $2i+7j+7k$and $3i+5j+7k$ respectively.

Complete step-by-step solution:
Now considering from the question we have been given that the position vectors of the vertices $A$ , $B$ and $C$ of the triangle $ABC$ are given as $4i+7j+8k$, $2i+7j+7k$ and $3i+5j+7k$ respectively.
The expressions representing the line $AB$ will be $\Rightarrow \left( 2i+7j+7k \right)-\left( 4i+7j+8k \right)=-2i-k$ .
The length of $AB$ will be given as $\left| AB \right|=\sqrt{{{1}^{2}}+{{2}^{2}}}\Rightarrow \sqrt{5}$ .
The expressions representing the line $AC$ will be $\Rightarrow \left( 3i+5j+7k \right)-\left( 4i+7j+8k \right)=-i-2j-k$ .
The length of $AC$ will be given as $\left| AC \right|=\sqrt{{{1}^{2}}+{{2}^{2}}+{{1}^{2}}}\Rightarrow \sqrt{6}$ .
The expressions representing the line $BC$ will be $\Rightarrow \left( 3i+5j+7k \right)-\left( 2i+7j+7k \right)=i-2j$ .
From the basic concepts of triangles, we know that the formula for finding $D$ the position vector of the point where the bisector of angle $A$ meets $BC$ is given as $\dfrac{\left| AB \right|\left( C \right)+\left| AC \right|\left( B \right)}{\left| AB \right|+\left| AC \right|}$ which is a section formula for vectors, where $B,C$ the position vectors of $B,C$ respectively. Now by applying the formula we will have
$\begin{align}
  & \Rightarrow \dfrac{\sqrt{5}\left( 3i+5j+7k \right)+\sqrt{6}\left( 2i+7j+7k \right)}{\sqrt{5}+\sqrt{6}} \\
 & \Rightarrow \dfrac{3\sqrt{5}i+2\sqrt{6}i+5\sqrt{5}j+7\sqrt{6}j+7\sqrt{5}k+7\sqrt{6}k}{\sqrt{5}+\sqrt{6}} \\
 & \Rightarrow \left( \dfrac{3\sqrt{5}+2\sqrt{6}}{\sqrt{5}+\sqrt{6}} \right)i+\left( \dfrac{5\sqrt{5}+7\sqrt{6}}{\sqrt{5}+\sqrt{6}} \right)j+\left( \dfrac{7\sqrt{5}+7\sqrt{6}}{\sqrt{5}+\sqrt{6}} \right)k \\
 & \Rightarrow \left( 2+\dfrac{\sqrt{5}}{\sqrt{5}+\sqrt{6}} \right)i+\left( 5+\dfrac{2\sqrt{6}}{\sqrt{5}+\sqrt{6}} \right)j+7k \\
 & \Rightarrow 2.477i+6.044j+7k \\
\end{align}$
 

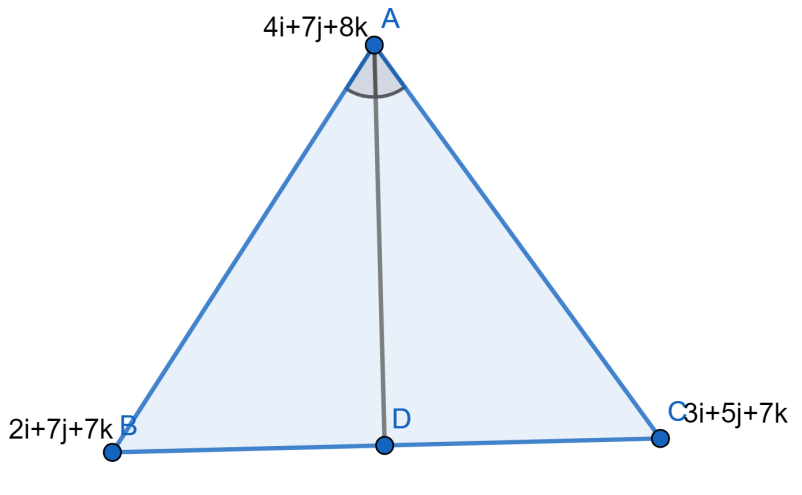
Therefore we can conclude that the position vector of the point where the bisector of angle $A$ meets $BC$ is given as $2.477i+6.044j+7k$ . Therefore we will mark the option “B” as correct.

Note: While answering questions of this type we should be sure with our concepts that we are going to apply during the process. If we have forgot and assumed the section formula to be $\dfrac{\left| AB \right|\left( B \right)+\left| AC \right|\left( C \right)}{\left| AB \right|+\left| AC \right|}$ ,then the result will be wrong.