Question

If the vectors $2i+4j-5k$ and $i+2j+3k$ are adjacent sides of a parallelogram, then the lengths of its diagonals are:
1) $7,\sqrt{69}$
2) $6,\sqrt{59}$
3) $5,\sqrt{65}$
4) $5,\sqrt{55}$

Answer 1

Hint: Here in this question we have been asked to find the length of the diagonals of the parallelogram having its adjacent sides as $2i+4j-5k$ and $i+2j+3k$ . For answering this question we will use the parallelogram law of vectors and the triangle law of vectors.

Complete step-by-step solution:
Now considering from the questions we have been asked to find the length of the diagonals of the parallelogram having its adjacent sides as $2i+4j-5k$ and $i+2j+3k$ .
From the basic concepts of vectors, we have learnt the parallelogram law of vectors stated as “When the two adjacent sides of a parallelogram are given as $a$ and $b$ then the diagonal passing from the common point of the sides will be $a+b$”.
From the basic concepts of vectors, we have learnt the triangle law of vectors stated as “The sum of all three vectors representing three sides of the triangle will be zero”.

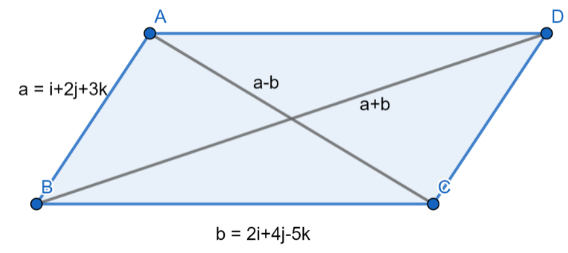
Let us assume that $2i+4j-5k=a$ and $i+2j+3k=b$ .
Hence we can conclude that the diagonals of the given parallelogram will be $a+b$ and $a-b$ .
$\begin{align}
  & a-b=2i+4j-5k-\left( i+2j+3k \right) \\
 & \Rightarrow a-b=i+2j-8k \\
\end{align}$
$\begin{align}
  & a+b=2i+4j-5k+\left( i+2j+3k \right) \\
 & \Rightarrow a+b=3i+6j-2k \\
\end{align}$
The length of the diagonal $a+b=3i+6j-2k$ will be given as
$\begin{align}
  & = \sqrt{{{3}^{2}}+{{6}^{2}}+{{2}^{2}}} \\
&=\sqrt{9+36+4} \\
 & =7 \\
\end{align}$
The length of the diagonal $a-b=i+2j-8k$ will be given as
$\begin{align}
  & = \sqrt{{{1}^{2}}+{{2}^{2}}+{{8}^{2}}}\\
 & =\sqrt{1+4+64} \\
 & = \sqrt{69} \\
\end{align}$
Hence we can conclude that the length of the diagonals of the parallelogram having its adjacent sides as $2i+4j-5k$ and $i+2j+3k$ will be given as $7,\sqrt{69}$ .
Hence we will mark the option “1” as correct.

Note: This is a very easy question and can be answered in a short span of time. Very few mistakes are possible in questions of this type. Someone can make a calculation mistake and consider the length of$\left| a+b \right|$ as 6 which will lead them to mark the wrong option.