Question

If the sum of the diagonals of a rhombus is 12cm and its perimeter is $8\sqrt{5}cm$ then lengths of the diagonal are:
A.6cm and 6cm
B.7cm and 5cm
C.8cm and 4cm
D.9cm and 3cm

Answer 1

Hint: Let us suppose that the length of one of the diagonals is “a” and the length of the other diagonal is “b”. Now, sum of the diagonals are given as 12cm so equating the addition of a and b to 12 we get $a+b=12$. Mark this equation as 1. From the perimeter of the rhombus we can find the side of the rhombus by dividing the perimeter by 4 so the side of the rhombus is $2\sqrt{5}$.We know that the diagonals of a rhombus bisect each other at ${{90}^{0}}$ so the diagonals are cutting 4 right angled triangles using the two half diagonals and a side so using the Pythagoras theorem make a relation between “a”, “b” and the side of the rhombus. Now, we have two equations in “a” and “b”, one equation comes from the Pythagoras theorem and the other is eq. (1) so solving these two equations will give the values of “a” and “b”.

Complete step-by-step answer:
In the below figure, we have shown a rhombus ABCD with two diagonals.

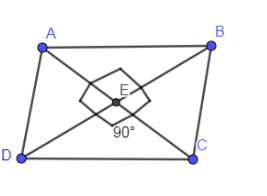
Let us assume that the diagonal AC is equal to “a” and the diagonal BD is equal to “b”.
It is given that the sum of the diagonals equal to 12cm.
$a+b=12cm$……… Eq. (1)
It is given that the perimeter of the rhombus is $8\sqrt{5}cm$ and we know that all the sides of the rhombus are equal so let’s name the side of the rhombus as “r”.
$\begin{align}
  & 4r=8\sqrt{5} \\
 & \Rightarrow r=2\sqrt{5} \\
\end{align}$
From the above, the side of the rhombus is equal to $2\sqrt{5}cm$.
We know that the diagonals of the rhombus bisect each other at ${{90}^{0}}$ so the diagonals of the rhombus cut the rhombus in 4 right angled triangles.

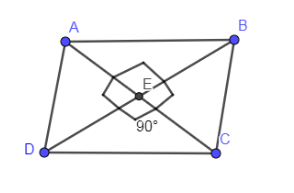
Let us take the right triangle $\Delta DEC$ and applying Pythagoras theorem on this triangle we get,
${{\left( DC \right)}^{2}}={{\left( DE \right)}^{2}}+{{\left( EC \right)}^{2}}$
As diagonals bisect each other so the length of the side DE is equal to $\dfrac{b}{2}$ and length of the side EC is equal to $\dfrac{a}{2}$ and as DC is the side of the rhombus that we have found above is equal to $2\sqrt{5}$. Now, substituting these values in the above equation we get,
$\begin{align}
  & {{\left( 2\sqrt{5} \right)}^{2}}={{\left( \dfrac{b}{2} \right)}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}} \\
 & \Rightarrow 20=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\
\end{align}$
On cross-multiplication the above equation we look like:
$80={{a}^{2}}+{{b}^{2}}$ ……….. Eq. (2)
From eq. (1) we can write “a” in terms of “b” as follows:
$\begin{align}
  & a+b=12 \\
 & \Rightarrow a=12-b \\
\end{align}$
Substituting the above value of “b” in eq. (2) we get,
$80={{\left( 12-b \right)}^{2}}+{{b}^{2}}$
$\begin{align}
  & \Rightarrow 80=144+{{b}^{2}}-24b+{{b}^{2}} \\
 & \Rightarrow 2{{b}^{2}}-24b+64=0 \\
\end{align}$
Dividing 2 on both the sides we get,
${{b}^{2}}-12b+32=0$
Solving the above quadratic equation by factorization method we get,
$\begin{align}
  & {{b}^{2}}-8b-4b+32=0 \\
 & \Rightarrow b\left( b-8 \right)-4\left( b-8 \right)=0 \\
 & \Rightarrow b=4,8 \\
\end{align}$
Substituting the value of “b” in eq. (1) we get,
$a+b=12cm$
Substituting the value of $b=4$ in the above equation we get,
$\begin{align}
  & a+4=12 \\
 & \Rightarrow a=8 \\
\end{align}$
Substituting the value of $b=8$ in the above equation we get,
$\begin{align}
  & a+8=12 \\
 & \Rightarrow a=4 \\
\end{align}$
From the above solution, we have two pair of a & b values.
$\begin{align}
  & a=4,b=8 \\
 & a=8,b=4 \\
\end{align}$
On matching the values of a & b that we have got above to the options the correct answer is option (c).

Note: In the step where we have applied Pythagoras Theorem,
${{\left( DC \right)}^{2}}={{\left( DE \right)}^{2}}+{{\left( EC \right)}^{2}}$
${{\left( 2\sqrt{5} \right)}^{2}}={{\left( \dfrac{b}{2} \right)}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}$

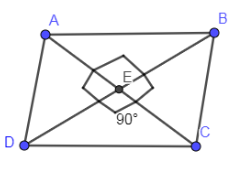
Instead of writing the value of half diagonals as half of “a” and half of “b”, you can check the options one by one. First of all half the value of diagonals given in the option then put these values in place of DE & EC. In the below, we have taken one of the options and illustrating what we have just discussed.
Let us take option (a) i.e. 6cm and 6cm. First of all we are going to half these values which will give us 3cm and 3cm.
Then substituting the above values in ${{\left( DC \right)}^{2}}={{\left( DE \right)}^{2}}+{{\left( EC \right)}^{2}}$ we get,
 $\begin{align}
  & {{\left( 2\sqrt{5} \right)}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 3 \right)}^{2}} \\
 & \Rightarrow 20=9+9 \\
 & \Rightarrow 20=18 \\
\end{align}$
As L.H.S is not equal to R.H.S which means the option (a) is not correct.
Similarly, you can check for other options.