Question

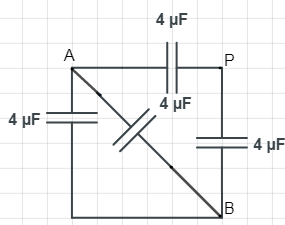
If the potential difference across AB is 5V find the charge on each capacitor.

Answer 1

Hint: The amount of charge into plates of capacitors depends upon the capacitance and the applied voltage charge is equal to the product of capacitance and the potential difference between the plates. Use the mathematical expression for the charge stored in the capacitor to get the required answer.
Formula used:
$\begin{align}
  & q=CV \\
 & {{C}_{Parallel}}={{C}_{1}}\,+\,{{\text{C}}_{2}} \\
 & {{C}_{Series}}=\dfrac{1}{\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}} \\
\end{align}$

Complete step-by-step solution
Capacitors are a combination of two conducting plates or conductors placed close to each other. One of the conductors is given a positive charge and the other is given an equal negative charge. The conductor with positive charge is called the positive plate and the other is called the negative plate.
We know that it is shown in figure that there are four capacitors each having same value of capacitance that is $4\mu F.$
Now, we give or assume the names of each capacitance to differentiate between them for easier calculations.

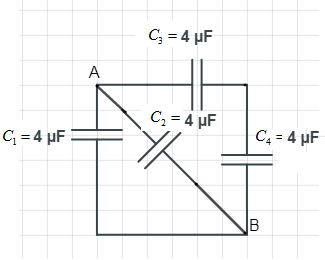
Using the formula of charge,
$q\,=\,CV$, where ‘q’ is charged, ‘C’ is the capacitance and ‘V’ is the potential difference between the plates.
We know that the voltage is similar for capacitors that are connected in parallel combination and the voltage is distributed for capacitors that are connected in series combination.
From the above diagram, it is clear that ${{C}_{1}}\,\text{and }{{\text{C}}_{2}}$ are connected in parallel and ${{C}_{3}}\,\text{and }{{\text{C}}_{4}}$ are connected in series but it is parallel to ${{C}_{1}}\,\text{and }{{\text{C}}_{2}}$.
So, the net capacitor value for the combination of ${{C}_{3}}\,\text{and }{{\text{C}}_{4}}$ is:
$\begin{align}
  & {{C}_{Net}}=\dfrac{1}{\dfrac{1}{{{C}_{3}}}+\dfrac{1}{{{C}_{4}}}} \\
 & \Rightarrow {{C}_{Net}}=\dfrac{1}{\dfrac{1}{4}+\dfrac{1}{4}} \\
 & \Rightarrow {{C}_{Net}}=\dfrac{1}{\dfrac{2}{4}} \\
 & \therefore {{C}_{Net}}=2\,\mu C \\
\end{align}$
So, ${{C}_{1}},\,{{C}_{2}}\,\text{and }{{\text{C}}_{Net}}$ are connected in parallel combination, so the voltage is similar along these capacitors.
Hence, the charge of the capacitor is:
${{q}_{1}}={{C}_{1}}V=4\times 5=20\mu C$
${{q}_{2}}={{C}_{2}}V=4\times 5=20\mu C$
And,
${{q}_{Net}}={{C}_{Net}}V=2\times 5=10\mu C$
Therefore, the charge across ${{C}_{1}}\,\text{and }{{\text{C}}_{2}}$ capacitor will be $20\,\mu C$ and charge across ${{C}_{3}}\,\text{and }{{\text{C}}_{4}}$ capacitor will be $10\,\mu C$ for a potential difference of $5\,V$.

Note: The main point to take care while solving this kind of problem is to check the type of connection the capacitor is in, as the voltage distribution will depend on the net capacitor value in that wire. There are two types of connections that are possible, which are parallel and series connection, and the voltage is the same in capacitors that are parallel to each other and distributed for capacitors that are in series connection to each other.