Question

If the points $\text{A(-2,-1)}\,\text{,}\,\text{B(1,0)}\,\text{,}\,\text{1(a,3)}\,\text{and}\,\text{D(1,b)}$ from a parallelogram ABCD , find the value of a and b .

Answer 1

Hint: In the question, we have been given the four vertices of a parallelogram. First, we draw a rough sketch and you can see the midpoints of AC and BD coincide. so we use the property of parallelogram that diagonals bisect each other and with the distance two points formula, we can solve the question.

Complete step by step solution:

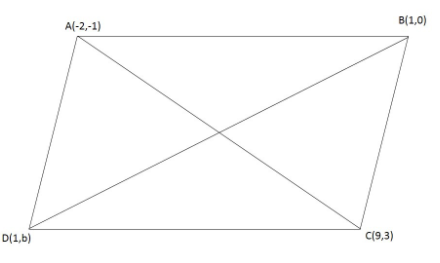
Now, as we can see the diagonals of the parallelogram bisect each other.
This means that the mid – point of the diagonal AC coincide with the mid point of the diagonal BD .
$\therefore $ Midpoint of formula for two points
     \[\begin{align}
  & \text{(}{{\text{x}}_{\text{1}}}\,\text{,}\,{{\text{y}}_{\text{1}}}\text{)}\,\text{ }\!\!\And\!\!\text{ }\,\text{(}{{\text{x}}_{\text{2}}}\,\text{,}\,{{\text{y}}_{\text{2}}}\text{)}\,\text{is} \\
 & \text{(x}\,\text{,}\,\text{y)}\,\text{=}\,\left( \dfrac{{{\text{x}}_{\text{1}}}\,\text{+}\,{{\text{x}}_{\text{2}}}}{\text{2}}\,\text{,}\,\dfrac{{{\text{y}}_{\text{1}}}\,\text{+}\,{{\text{y}}_{\text{2}}}}{\text{2}} \right) \\
 & \text{=}\,\left( \dfrac{\text{a-2}}{\text{2}}\,\text{,}\,\text{1} \right) \\
 & \text{Now}\,\text{,}\,\text{mid-point}\,\text{of}\,\text{BD}\,\text{=}\,\left( \dfrac{\text{1+1}}{\text{2}}\,\text{+}\,\dfrac{\text{b+0}}{\text{2}} \right) \\
 & \text{=}\,\left( \dfrac{\text{2}}{\text{2}}\,\text{,}\,\dfrac{\text{b}}{\text{2}} \right) \\
 & \text{=}\,\left( \text{1}\,\text{,}\dfrac{{}}{\text{2}} \right)\text{.}
\end{align}\]
Now , as we know ,
Midpoint of AC = midpoint of BD
     \[\dfrac{\text{a-2}}{\text{2}}\,\text{=}\,\text{1}\,\text{and}\,\text{1}\,\text{=}\dfrac{\text{b}}{\text{2}}\]
Solving the above equation ,
     \[\begin{align}
  & \text{a -2}\,\text{=}\,\text{2}\,\text{and}\,\text{2}\,\text{=}\,\text{b} \\
 & \text{a}\,\text{=}\,\text{2+2} \\
 & \text{a}\,\text{=}\,\text{4}\,\text{and}\,\text{b}\,\text{=2} \\
 &
\end{align}\]

Hence ,$\text{a}\,\text{=}\,\text{4}\,\text{and}\,\text{b=}\,\text{2}$

Note: Basic important properties of parallelogram are :
(1) opposite sides are congruent.
(2) opposite angles are congruent.
(3) consecutive angles are supplementary.
(4) If one angle is right, then all angles are right
(5) Diagonals bisect each other.