
If the point \[\hat{i}+\hat{j}\] , \[\hat{i}-\hat{j}\] and $p\hat{i}+q\hat{j}+r\hat{k}$ are collinear, then
$\begin{align}
& a)p=1 \\
& b)r=0 \\
& c)q\in R \\
& d)q\ne 1 \\
\end{align}$
Answer
576.9k+ views
Hint: Now we know that the given points are collinear. Let us say A = \[\hat{i}+\hat{j}\] , C = \[\hat{i}-\hat{j}\] and B = $p\hat{i}+q\hat{j}+r\hat{k}$. Now we know that the angle between AC and BC is 0. Hence we will take the cross product of AB and BC. Hence we will find the required condition.
Complete step by step answer:
Now let us consider the three point A = \[\hat{i}+\hat{j}\] , C = \[\hat{i}-\hat{j}\] and B = $p\hat{i}+q\hat{j}+r\hat{k}$ . We know that the points are collinear.
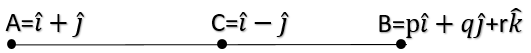
Now we know first let us calculate CA.
CA = $\hat{i}-\hat{j}-\left( \hat{i}+\hat{j} \right)=-2\hat{j}$
Now let us calculate BC.
$BC=p\hat{i}+q\hat{j}+r\hat{k}-\left( \hat{i}-\hat{j} \right)=\left( p-1 \right)\hat{i}+\left( q+1 \right)\hat{j}+r\hat{k}$
Now we know that ABC are collinear hence the angle between AC and BC is 0.
Now we know that $AC\times BC=|AB||BC|\sin \theta $
Here we have the angle is 0. Hence we get $\sin \theta =0$
Now we have \[AC\times BC=0\]
Hence we have $\left( -2\hat{j} \right)\times \left[ \left( p-1 \right)\hat{i}+\left( q+1 \right)\hat{j}+r\hat{k} \right]=0$
Now we know that $\hat{j}\times \hat{i}=-\hat{k}$, $\hat{j}\times \hat{j}=0$ and $\hat{j}\times \hat{k}=\hat{i}$
Hence we get,
$\left[ -\left( -2p+2 \right)\hat{k}+\left( 0 \right)+\left( -2r \right)\hat{i} \right]=0$
Hence we have $2r=0$ and $-2p+2=0$
Now consider 2r = 0.
Dividing the equation by 2 we get, r = 0.
Now consider the equation -2p + 2 = 0
Now rearranging the terms we get, 2p = 2
Dividing the whole equation by 2 we get p = 1.
Hence we get, p = 1 and r = 0.
Now there is no condition on q hence we can say that $q\in R$
So, the correct answer is “Option A, B and C”.
Note: Now note that for any two vectors we have if the vectors are perpendicular their dot product is 0 and if they are parallel the cross product is 0. Also in general we can calculate cross product of two vectors $a\hat{i}+b\hat{j}+c\hat{k}$ and $p\hat{i}+q\hat{j}+r\hat{k}$ is given by $\left| \begin{matrix}
{\hat{i}} & {\hat{j}} & {\hat{k}} \\
a & b & c \\
p & q & r \\
\end{matrix} \right|=0$ .
Complete step by step answer:
Now let us consider the three point A = \[\hat{i}+\hat{j}\] , C = \[\hat{i}-\hat{j}\] and B = $p\hat{i}+q\hat{j}+r\hat{k}$ . We know that the points are collinear.
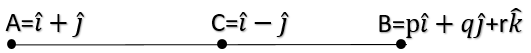
Now we know first let us calculate CA.
CA = $\hat{i}-\hat{j}-\left( \hat{i}+\hat{j} \right)=-2\hat{j}$
Now let us calculate BC.
$BC=p\hat{i}+q\hat{j}+r\hat{k}-\left( \hat{i}-\hat{j} \right)=\left( p-1 \right)\hat{i}+\left( q+1 \right)\hat{j}+r\hat{k}$
Now we know that ABC are collinear hence the angle between AC and BC is 0.
Now we know that $AC\times BC=|AB||BC|\sin \theta $
Here we have the angle is 0. Hence we get $\sin \theta =0$
Now we have \[AC\times BC=0\]
Hence we have $\left( -2\hat{j} \right)\times \left[ \left( p-1 \right)\hat{i}+\left( q+1 \right)\hat{j}+r\hat{k} \right]=0$
Now we know that $\hat{j}\times \hat{i}=-\hat{k}$, $\hat{j}\times \hat{j}=0$ and $\hat{j}\times \hat{k}=\hat{i}$
Hence we get,
$\left[ -\left( -2p+2 \right)\hat{k}+\left( 0 \right)+\left( -2r \right)\hat{i} \right]=0$
Hence we have $2r=0$ and $-2p+2=0$
Now consider 2r = 0.
Dividing the equation by 2 we get, r = 0.
Now consider the equation -2p + 2 = 0
Now rearranging the terms we get, 2p = 2
Dividing the whole equation by 2 we get p = 1.
Hence we get, p = 1 and r = 0.
Now there is no condition on q hence we can say that $q\in R$
So, the correct answer is “Option A, B and C”.
Note: Now note that for any two vectors we have if the vectors are perpendicular their dot product is 0 and if they are parallel the cross product is 0. Also in general we can calculate cross product of two vectors $a\hat{i}+b\hat{j}+c\hat{k}$ and $p\hat{i}+q\hat{j}+r\hat{k}$ is given by $\left| \begin{matrix}
{\hat{i}} & {\hat{j}} & {\hat{k}} \\
a & b & c \\
p & q & r \\
\end{matrix} \right|=0$ .
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




