Question

If the perimeter of a rhombus is 20 cm and one of its diagonals is 8 cm, then find the area of the rhombus.

Answer 1

Hint: In this question, we use the property of rhombus that is the diagonals of a rhombus bisect each other at right angles ${90^0}$ and also use the formula of area of rhombus. Area of rhombus $ = \dfrac{{{d_1} \times {d_2}}}{2}$ , where d1 and d2 are diagonals of rhombus.

Complete step-by-step answer:
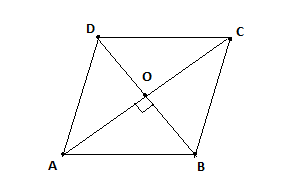
Consider a rhombus ABCD in which the length of one diagonal $AC = {d_1} = 8cm$ and the perimeter of the rhombus is 20cm.
Let the side of the rhombus be a cm and the length of the other diagonal is ${d_2}$.
Given, Perimeter of rhombus =20cm

Formula of perimeter of rhombus is 4a where a is the side of rhombus.
\[
  {\text{Perimeter of rhombus}} = 20 \\
   \Rightarrow 4a = 20 \\
   \Rightarrow a = \dfrac{{20}}{4} \\
   \Rightarrow a = 5cm \\
\]
So, the side of the rhombus is 5cm.
Now, we know the diagonals of a rhombus bisect each other at right angles ${90^0}$ .
So, \[OA = OC = \dfrac{{{d_1}}}{2} = 4cm{\text{ and }}\angle AOB = \angle BOC = \angle COD = \angle DOA = {90^0}\]
Now, we apply Pythagoras theorem in $\vartriangle ABC$ where \[\angle AOB = {90^0}\] .
$ \Rightarrow {\left( {AB} \right)^2} = {\left( {OA} \right)^2} + {\left( {OB} \right)^2}$
Side of rhombus, a=AB=5cm
$
   \Rightarrow {\left( 5 \right)^2} = {\left( 4 \right)^2} + {\left( {OB} \right)^2} \\
   \Rightarrow {\left( {OB} \right)^2} = 25 - 16 \\
   \Rightarrow OB = \sqrt 9 = 3cm \\
$
Now, we know the diagonals of a rhombus bisect each other.
\[
   \Rightarrow OB = OD = \dfrac{{{d_2}}}{2} \\
   \Rightarrow {d_2} = OB \times 2 \\
   \Rightarrow {d_2} = 3 \times 2 \\
   \Rightarrow {d_2} = 6cm \\
 \]
Now, we apply area of rhombus $ = \dfrac{{{d_1} \times {d_2}}}{2}$
\[
   \Rightarrow {\text{Area of rhombus}} = \dfrac{{8 \times 6}}{2} \\
   \Rightarrow {\text{Area of rhombus}} = \dfrac{{48}}{2} \\
   \Rightarrow {\text{Area of rhombus}} = 24c{m^2} \\
 \]
So, the area of rhombus is 24 $ c{m^2} $

Note: In such types of problems we have to use the property of diagonals of rhombus. First we find the side of the rhombus by using the perimeter of the rhombus and then find the length of the other diagonal by using Pythagoras theorem. So, after applying the formula of the area of the rhombus we will get the required answer.