Question

If the normal drawn at the end points of a variable chords PQ of the parabola \[{{y}^{2}}\ =\ 4ax\] intersect a parabola, then the locus of the point of intersection of the tangent drawn at the points P and Q is
\[x+a\ =\ 0\]
\[x-2a\ =\ 0\]
 \[{{y}^{2}}-4x+6\ =\ 0\]
\[{{y}^{2}}+4x-6\ =\ 0\]

Answer 1

Hint: We will be using the concepts of parabola to solve the problem. We will also be using concepts of tangent, chords of parabola to further simplify the problem.

Complete step by step answer:
Now, we have been given that the normal drawn at the end points of variable chord PQ intersect a parabola. So, we will draw the diagram accordingly.

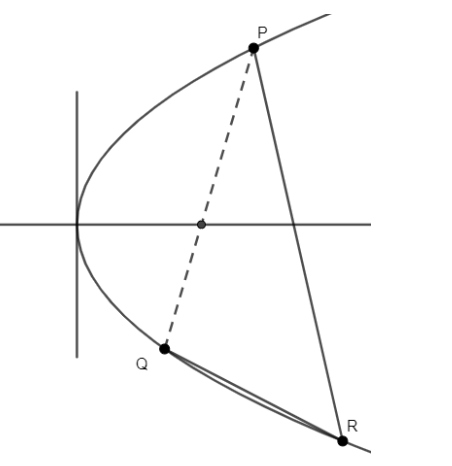
Now, we know that whenever the normal drawn at the ends of a chord intersects a parabola the chord is a focal chord means that the chord passes through the focus. Therefore, PQ is a focal chord.
Now, we will draw the directrix of the parabola \[{{y}^{2}}\ =\ 4ax\]. We know that the equation of the directrix is \[x\ =\ -a\]and the coordinate of focus is \[\left( -a,0 \right)\].

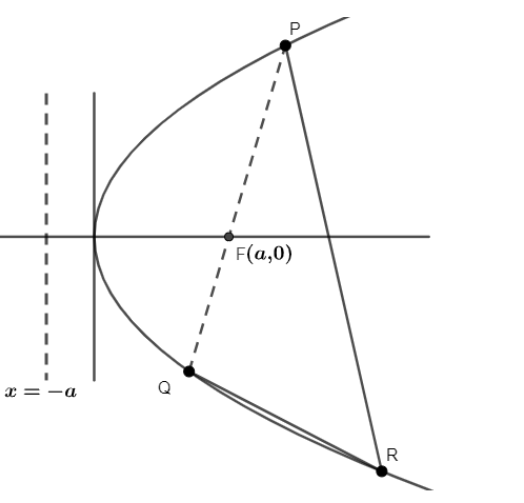
Now, we will take a point on the directrix, let the point be \[\left( -a,c \right)\] where \[c\ \in \ \text{R}\]. Now, we will write the equation of chord of contact for point \[\left( -a,c \right)\]. We know that the equation of chord of contact is \[\text{T}\ \text{=}\ \text{0}\]. Where T is
\[yy'-\dfrac{4a\left( x+x' \right)}{2}\ =\ 0\]
See now, \[y'x'\ =\ \left( -a,c \right)\]
 \[yc-\dfrac{4a\left( x-a \right)}{2}\ =\ 0\]
\[yc-2a\left( x-a \right)\ =\ 0\] …………………………………..(i)
Now, we see that the coordinate \[\left( a,0 \right)\]or Focus satisfy (i),
\[y0-2a\left( a-a \right)\ =\ 0\]
\[0\ =\ 0\]
Now, we can say that locus of point of intersection of the tangent drawn at P, Q is \[x-a\] because we have proved that the chord is focal chord and also we have taken an arbitrary point on directrix and proved that chord of contact is focal chord so the vice-versa will also be true hence the tangents drawn at point P and Q is \[x\ =\ -a\] or \[x\ +a\ =\ 0\].
Hence, option (a) is correct.

Note: To solve these types of questions one must have a good understanding of parabola and its properties. Properties of the directrix of parabola and focal chord of parabola are important to solve such questions.