Question

If the non-parallel sides of a trapezium are equal, prove that the trapezium is cyclic.

Hint: For a cyclic quadrilateral, the sum of the pair of opposite angles is ${180^ \circ }$. Use this result to prove the trapezium is cyclic.

Answer 1

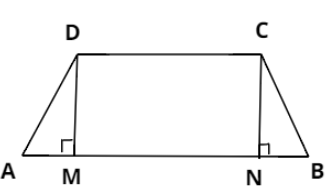
Consider trapezium ABCD such that AB is parallel to CD and $AD = BC$.
Consider two points M and N that can be considered as the foot of perpendicular drawn on AB from vertices D and C respectively.
Now, if we compare $\Delta DAM$and $\Delta CBN$, we have:
$AD = BC{\text{ }}...{\text{(Given)}}$
$\angle AMD = \angle BNC{\text{ }}...{\text{(Right angles i}}{\text{.e}}{\text{. 9}}{{\text{0}}^ \circ }{\text{)}}$
And $DM = CN{\text{ }}....{\text{(Distance between two parallel lines)}}$
From this we can say that both the triangles are congruent.
$\Delta DAM \cong \Delta CBN$
We know that corresponding parts of congruent triangles are equal. So we have:
$ \Rightarrow \angle A = \angle B .....(i)$
Also $\angle B + \angle C = {180^ \circ }{\text{ }}...{\text{(sum of co - interior angles)}}$
Substituting the value of $\angle B$ from equation first, we have:
$ \Rightarrow \angle A + \angle C = {180^ \circ } ....(ii)$
Equation $(ii)$ shows that the sum of the pair of opposite angles of trapezium ABCD is ${180^ \circ }$.
Therefore the trapezium is a cyclic quadrilateral.
Note: A quadrilateral is said to be cyclic quadrilateral if all of its 4 vertices lie on the same circle.