Question

If the length of the wire is doubled and its area of cross section is decreased to half, then its resistance
(A) Will increase 4 times
(B) Will become double
(C) Will remain the same as before
(D) Will become half the initial value.

Answer 1

Hint
The resistance of the conductor is given by, Substitute the initial and final values and obtain the resistance for the two cases. Compare final resistance with initial resistance to know by how much the resistance has changed.

Complete step-by-step solution
The property of a substance by virtue of which it opposes the current flowing through it is called resistance. It is given by,
$R = \rho \dfrac{l}{A}$
Where, $\rho $ is the resistivity of the material of the conductor.
From the above equation we know that,
$R \propto l$ and $R \propto \dfrac{1}{A}$
Let ${l_i}$ and ${l_f}$; ${A_i}$ and \[{A_f}\]be the initial and final values of length and area of cross section respectively.

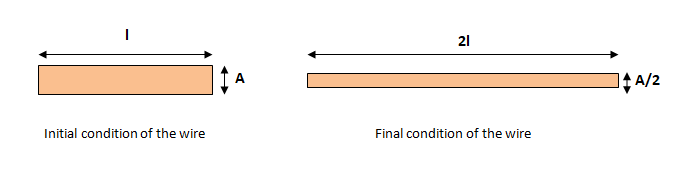
Given:
${l_i} = l$
${l_f} = 2l$
${A_i} = A$
\[{A_f} = \dfrac{A}{2}\]
For the initial conditions the resistance is
${R_f} = \rho \dfrac{l}{A} \to (1)$
For the final conditions the resistance is
${R_f} = \rho \dfrac{2l}{A/2} \to (2)$
From equation $(1)\,and\,(2)$
${R_f} = \rho \dfrac{{4l}}{A}$
${R_f} = 4{R_i}$
Hence, the final resistance is four times the initial resistance.
The correct option is (A).

Note
Here, resistivity of the conductor does not alter as it depends on the material of the conductor. Resistance also depends on the temperature. It is directly proportional to the temperature. It is given by,
$R = {R_0}(1 + \alpha T)$
Where, $\alpha $ is the temperature coefficient of resistance.