Question

If the length of the rectangle is increased by 25% and the breadth is decreased by 20%, then at what percentage the area decreases or increases?
(a) 20% increase
(b) 25% increase
(c) 25% decrease
(d) None of the above.

Answer 1

Hint: We solve this problem by using the area formula of a rectangle.
The formula of area of rectangle is given as
\[\Rightarrow \text{Area}=\left( length \right)\left( breadth \right)\]
By using this formula we calculate both old and new areas of the rectangle then we find the percentage increase or decrease. If the new area is larger than old then it has increased and if the new area is smaller than old then it has a decrease in area. We calculate the percentage as
\[Percentage=\dfrac{\left| \text{New area}-\text{original area} \right|}{\text{old area}}\times 100\]

Complete step by step answer:

Let us assume that the length of original rectangle as \['l'\]
We are given that the length has increased by 25%
Let us assume that the length of new rectangle as \['L'\] then we get
\[\Rightarrow L=l+\dfrac{25}{100}\times l\]
By adding the terms using the LCM in above equation we get
\[\Rightarrow L=\dfrac{5}{4}l\]
Now, let us assume that the breadth of original rectangle as \['b'\]
We are given that the breadth is decreased by 20%
Let us assume that the breadth of new rectangle as \['B'\] then we get
\[\begin{align}
  & \Rightarrow B=b-\dfrac{20}{100}\times b \\
 & \Rightarrow B=\dfrac{4}{5}b \\
\end{align}\]

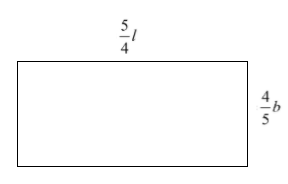
We know that the formula of area of rectangle is given as
\[\Rightarrow \text{Area}=\left( length \right)\left( breadth \right)\]
Let us assume that the area of original rectangle as \[{{A}_{1}}\] then by using the above formula we get
\[\begin{align}
  & \Rightarrow {{A}_{1}}=l\times b \\
 & \Rightarrow {{A}_{1}}=lb \\
\end{align}\]
Now, let us assume that the area of new rectangle as \[{{A}_{2}}\] then by using the area formula we get
\[\Rightarrow {{A}_{2}}=L\times B\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow {{A}_{2}}=\left( \dfrac{5}{4}l \right)\left( \dfrac{4}{5}b \right) \\
 & \Rightarrow {{A}_{2}}=lb \\
\end{align}\]
Here, we can see that the original area and new area are equal.
So we can say that there is no increase or decrease in percentage of area.

So, the correct answer is “Option d”.

Note: : Students may make mistakes in calculating the new length and breadth.
We have the new breadth after decreasing 20% as
\[\Rightarrow B=b-\dfrac{20}{100}\times b\]
But, in hurry or confusion students may assume the increase and decrease as same and take the breadth as
\[\Rightarrow B=b+\dfrac{20}{100}\times b\]
This gives the wrong answer because decrease in breadth means we need to subtract, we should not add. Also, the increase means that we need to add, we should not subtract.