Question

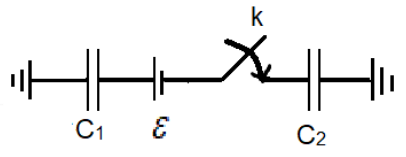
If the key $k$ is closed, find the charge that will flow through the capacitors.

A. $\sqrt {{C_1}{C_2}} \varepsilon $
B. $\dfrac{{{C_1}{C_2}\varepsilon }}{{{C_1} + {C_2}}}$
C. $\left( {{C_1} + {C_2}} \right)\varepsilon $
D. zero

Answer 1

Hint:Capacitors store energy through charging and discharging cycles and hold this energy in the electric field between its plates even after disconnecting the supply voltage which is what makes it very useful. The equivalent capacitance of the circuit is calculated by the capacitor in series formula and the relation between the capacitance and charge is applied in-order to determine the charge through both of the capacitors in the circuit.

Formula used:
The formula for the total charge of the capacitor is:
$q = CV$
Where, $q$ is the charge acquired, $C$ is the capacitance, $V$ is the potential difference of the circuit.
For a series combination of $n$ capacitors we have the formula:
$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + .... + \dfrac{1}{{{C_n}}}$
Where, ${C_s}$ is the equivalent series capacitance and ${C_1},{C_2},...{C_n}$ are individual capacitances.

Complete step by step answer:
We are well aware that capacitors are devices that store energy and this energy is stored in the form of charge. The aim here is to find the charge that flows through the capacitors.Charge can only be stored in the capacitors when a certain amount of current flows through the circuit per unit time.

For this the circuit must be complete or closed to provide a path for current to flow. This means that the current will only flow when the key $k$ is closed to form a closed circuit. Once the key is closed a potential difference is produced due to the supply voltage and hence due to the current produced the charge starts to build up in both the capacitors through its charging cycles.

From the diagram, we can see that one of the plates of the capacitors are grounded or earthed. This is done in-order to fix the amount of charge in one of the plates in accordance with the charge in the other plate. We know that the ground is like a sink with an infinite amount of charges flowing into and out of it. The charges flow into the plates to neutralize the charge acquired in the other plate and hence it is required to be grounded.

Knowing this concept, we construct the equation for the charge flowing through a capacitor. This equation is as follows:
$q = CV$
It can be seen that the circuit in the above diagram includes two capacitors and hence the total capacitance needs to be found out. Hence the above equation becomes:
$q = {C_{eq}}V$ -----($1$)
Here, ${C_{eq}}$ stands for the equivalent capacitance, that is, the total capacitance of both of the capacitors. In-order to find out the equivalent capacitance we first need to apply the formula for the capacitance in series as these two capacitors are connected in series with each other. It is given by the equation:
$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + .... + \dfrac{1}{{{C_n}}}$
The equation shows that the reciprocal of the equivalent capacitance is equal to the sum of the reciprocals of the individual capacitances.

Since there are only two capacitors in the circuit the equation becomes:
$\dfrac{1}{{{C_s}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
The variable ${C_s}$ can be substituted with the equivalent capacitance of the circuit ${C_{eq}}$.
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
We then obtain the equation for the equivalent capacitance taking its LCM and reciprocating it. We get:
${C_{eq}} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}}$ -----($2$)
Now that we have the value for ${C_{eq}}$ we substitute this equation ($2$) in ($1$).
$q = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} \times V$
The variable $V$ is the potential difference of the circuit which is given by the variable $\varepsilon $ as per the diagram. Hence we get the final equation to be:
$q = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} \times \varepsilon $
Hence the charge flowing through the capacitors when key is closed is $\dfrac{{{C_1}{C_2}\varepsilon }}{{{C_1} + {C_2}}}$.

Therefore, the correct option is option B.

Additional information: The capacitance is given to be the charge required to increase the potential of the conductor by a unit amount. For a series combination of capacitors the equivalent capacitance is always smaller than that of the individual capacitances. An important point to note is that the charge on each of these capacitors are the same since they are connected in series to each other.

The potential difference across any capacitor is inversely proportional to its capacitance.The capacitance is a measure of its capacity to hold large amounts of charge without running a high potential, that is, even after disconnecting the supply voltage. It depends on the size and shape of the conductor and the nature of the surrounding medium.

Note:Capacitors do not allow the flow of current through them due to the insulation between their plates as their role is to only build and store charges which increase with an increase with an increase in electric field induced between its plates. Capacitors usually block the flow of dc current when connected to a dc voltage supply but here we are asked to find the charge stored by the capacitors. There is often a misconception that since current does not flow through the capacitors there is no charge stored by it which is wrong.