Question

If the focus of a parabola divided a focal chord of the parabola in segments of length $3$ and$2$ the length of the latus rectum of the parabola is?
A) $\dfrac{3}{2}$
B) $\dfrac{6}{5}$
C) $\dfrac{12}{5}$
D) $\dfrac{24}{4}$

Answer 1

Hint: A parabola is a U-shaped plane curve where any point is at an equal distance from a fixed point (known as the focus) and from a fixed straight line which is known as the directrix. Actually parabola is an integral part of the conic section. The above given question is related to the parabola. Latus rectum is used in the given question. The latus rectum of a parabola is the chord that passes through the focus and is perpendicular to the x-axis of the parabola. Now what is a focal chord? Any chord passes through the focus of the parabola is a fixed chord of the parabola.

Complete step by step solution:
Let's draw a parabola with focus G.

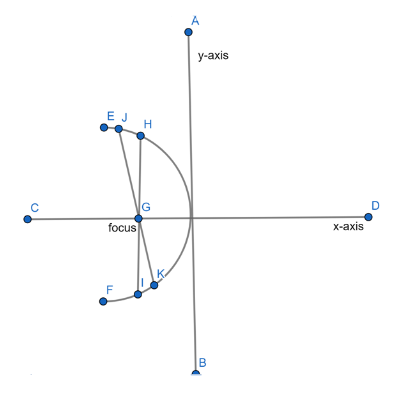
In this parabola HI is a latus rectum and JK is focal chord which is passing through the focus of the parabola.
To solve the given question let`s G(a,0) be the focus of the given parabola. And let the endpoints of the focal chord be $J\left( a{{t}^{2}},2at \right)$ and $K\left( \dfrac{a}{{{t}^{2}}},\dfrac{-2a}{t} \right)$ .
We know focus divides the focal length two parts. So GJ and GK are of equal length with length let c and d respectively.
 The length of the focal chord from the focus is given as $c=3$ and $d=2$
We know to find out the focal chord we have,
\[\Rightarrow \sqrt{{{\left( x-a \right)}^{2}}+{{y}^{2}}}=\left| \dfrac{x+a}{1} \right|\]
 So here $x=a{{t}^{2}}$ and$y=2at$ , then putting these in the above expression we get
\[\] $\Rightarrow GJ=\sqrt{{{\left( a-a{{t}^{2}} \right)}^{2}}+4{{a}^{2}}{{t}^{2}}}=a{{t}^{2}}+a=a\left( 1+{{t}^{2}} \right)$
Similarly, we can calculate GK as where $x=\dfrac{a}{{{t}^{2}}}$ and $y=\dfrac{-2a}{t}$
$\Rightarrow GK=\sqrt{{{\left( a-\dfrac{a}{{{t}^{2}}} \right)}^{2}}+\dfrac{4{{a}^{2}}}{{{t}^{2}}}}=a\left( \dfrac{{{t}^{2}}+1}{{{t}^{2}}} \right)$
And it is given that $GJ=3$ and $GK=2$
Now we have to find the length of the latus rectum which is a, for this we will write
$\begin{align}
  & \Rightarrow \dfrac{1}{GJ}+\dfrac{1}{GK}=\dfrac{1}{a} \\
 & \Rightarrow \dfrac{1}{GJ}+\dfrac{1}{GK}=\dfrac{1}{a\left( 1+{{t}^{2}} \right)}+\dfrac{{{t}^{2}}}{a\left( 1+{{t}^{2}} \right)}=\dfrac{1}{a} \\
 & \Rightarrow \dfrac{1}{GJ}+\dfrac{1}{GK}=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{1}{a} \\
\end{align}$
Now by more simplifying the above equation, we get
$\begin{align}
  & \Rightarrow \dfrac{1}{3}+\dfrac{1}{2}=\dfrac{3+2}{6}=\dfrac{5}{6}=\dfrac{1}{a} \\
 & \Rightarrow a=\dfrac{6}{5} \\
\end{align}$
Hence, the length of the latus rectum is $a=\dfrac{6}{5}$ .

Note: sometimes students get confused in parabola and hyperbola. The basic difference between parabola and hyperbola is that a parabola has a single focus and directrix , but hyperbola has two foci and two directrices. For the parabola the equation is ${{y}^{2}}=-4ax$ .