Question

If the focus of a parabola (− 2, 1) and equation of the directrix is x + y = 3, find the vertex of the parabola.

Answer 1

Hint: Here, use the concept that the vertex of a parabola is the midpoint of the focus of the parabola and the point where the directrix and the axis of parabola meets. Find the point of intersection of directrix and axis of parabola using the equation of directrix given.

Complete step-by-step answer:
As we know that the vertex of the parabola is the midpoint of the line segment joining the focus to the intersection point of the axis and its directrix.
In the figure below, B is the intersection point of the axis of parabola and the directrix of parabola then B is the foot of perpendicular drawn from the focus of parabola to the directrix of parabola.
Let the coordinate of B be (h, k).

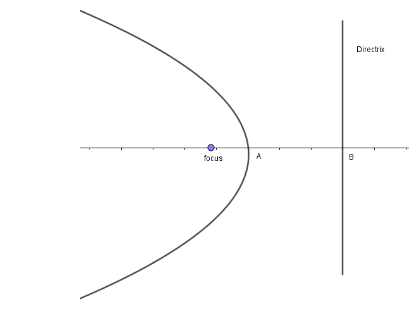
Given the equation of the directrix is y = − x + 3 and slope of the directrix is -1.
Since the axis is perpendicular to the directrix, therefore the slope of the axis is 1.
Equation of line passing through (-2, 1) and having slope 1 is
y – 1 = 1 × (x + 2) [Equation of line passing through (a, b) is given as y – b = m (x – a)]
x – y = − 3
Since point B lies on x is of parabola, therefore (h, k) must satisfy the equation of axis of parabola
h − k = − 3 …(i)
(h, k) also lies on the directrix so
h + k = 3 …(ii)
On adding equations (i) and (ii), we get
2h = 0 ⇒ h = 0
Putting value of h in equation (i), we get
0 – k = − 3 ⇒ k = 3
Therefore, vertex is mid-point of (− 2, 1) and (0, 3) i.e., (− 1, 2).

Note: In these types of questions, first draw the diagram of parabola and directrix to understand what to find. We must know the equation of the line passing through a point with a given slope.