Question

If the electric field to the right of two sheets is $\dfrac{{K\sigma }}{{{\varepsilon _0}}}$. Find $K$ ?
 

Answer 1

Hint: In order to solve this question we need to understand gauss law for electro statistics. According to gauss law, net flux enclosed by a closed surface is equal to net charge enclosed by surface divided by permittivity of free space ${\varepsilon _0}$ also the flux is equivalent to $\oint {\vec E.d\vec S} $. Here, $\vec E$ is an electric field and $d\vec S$ is an elemental area vector having direction normal to the plane of the surface. Using this we can calculate electric fields across any surface.

Complete step by step answer:
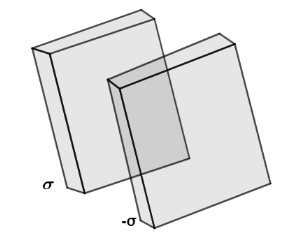
Consider a plane sheet of charge having surface charge distribution $\sigma $.Then using gauss law, we get electric field around sheet as,
$\vec E = \dfrac{\sigma }{{2{\varepsilon _0}}}\hat n$
Consider a point P in right side of both sheets, then electric field at P due to plane sheet of charge distribution is, ${E_1} = \dfrac{\sigma }{{2{\varepsilon _0}}}$ having direction away from each other. And, electric field at P due to plane sheet of charge distribution is, ${E_2} = \dfrac{{ - \sigma }}{{2{\varepsilon _0}}}$ having direction towards it.So from superposition principle, net electric field is due to,
$E = {E_1} + {E_2}$
$\Rightarrow E = \dfrac{\sigma }{{2{\varepsilon _0}}} + \dfrac{{ - \sigma }}{{2{\varepsilon _0}}}$
$\therefore E = 0$
So there is no electric field on the right side of both sheets.Comparing with the given value of $E$ in question we get, $K = 0$.

Note: It should be remembered that gauss law is only applicable for closed surfaces enclosing some net charge. Also the ${q_{net}}$ on right hand side of gauss law implies the total charge enclosed by surface whereas the term $E$ in left hand side of gauss law implies electric field and it is due to all charges on interior, exterior or on the closed surface.