Question

If the adjacent sides of a triangle are represented by the vectors \[\hat i + 2\hat j + 2\hat k\] and \[3\hat i - 2\hat j + \hat k\], then the area of the triangle is
A) \[\dfrac{{\sqrt {66} }}{2}\]
B) \[\dfrac{{\sqrt {116} }}{3}\]
C) \[\dfrac{{\sqrt {56} }}{2}\]
D) \[\dfrac{{\sqrt {116} }}{2}\]

Answer 1

Hint: The magnitude of the product is by definition the area of a parallelogram spanned by when placed tail-to-tail.
Formula used:
The cross product of two vectors is given by the following formula
\[\overrightarrow a \times \overrightarrow b = \left[ {\begin{array}{*{20}{c}}
  {\hat i}&{\hat j}&{\hat k} \\
  {{a_1}}&{{a_2}}&{{a_3}} \\
  {{b_1}}&{{b_2}}&{{b_3}}
\end{array}} \right]\] , where \[
  \overrightarrow a = {a_1}\hat i + {a_2}\hat j + {a_3}\hat k \\
  \overrightarrow b = {b_1}\hat i + {b_2}\hat j + {b_3}\hat k \\
 \]
The magnitude of a vector is given by the formula,
\[\left| {\overrightarrow {AB} } \right| = \sqrt {{m_1}^2 + {m_2}^2 + {m_3}^2} \], where\[\overrightarrow {AB} = {m_1}\hat i + {m_2}\hat j + {m_3}\hat k\].
In the cross
Hence we can use the vector product to compute the area of a triangle formed by three points A, B and C in space.

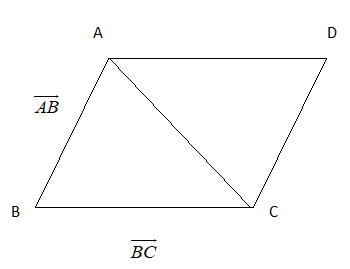
It follows that the area of the triangle ABC is given by the formula \[\dfrac{1}{2}\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right|\]
Complete step-by-step answer:
It is given that the adjacent sides of a triangle are represented by the vectors \[\hat i + 2\hat j + 2\hat k\] and \[3\hat i - 2\hat j + \hat k\] respectively.
Let us consider the vectors as
 \[\overrightarrow {AB} = \hat i + 2\hat j + 2\hat k\]
\[\overrightarrow {BC} = 3\hat i - 2\hat j + \hat k\]
We know that, if \[\overrightarrow {AB} \]and \[\overrightarrow {BC} \]are the adjacent sides of a triangle, then the area of the triangle ABC is given by the formula mentioned in the hint.
Now to use the formula of area of triangle we are in need to find\[\overrightarrow {AB} \times \overrightarrow {BC} \],
Hence,
 \[\overrightarrow {AB} \times \overrightarrow {BC} = \left[ {\begin{array}{*{20}{c}}
  {\hat i}&{\hat j}&{\hat k} \\
  1&2&2 \\
  3&{ - 2}&1
\end{array}} \right]\]
Using the matrix we get,
\[
  \left[ {\begin{array}{*{20}{c}}
  {\hat i}&{\hat j}&{\hat k} \\
  1&2&2 \\
  3&{ - 2}&1
\end{array}} \right] = \hat i\{ 2 \times 1 - 2 \times ( - 2)\} - \hat j(1 \times 1 - 2 \times 3) + \hat k\{ 1 \times ( - 2) - 2 \times 3\} \\
   = \hat i(2 + 4) - \hat j(1 - 6) + \hat k( - 2 - 6) \\
   = 6\hat i + 5\hat j - 8\hat k \\
 \]
Thus now let us find \[\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right|\]
\[\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right| = \left| {6\hat i + 5\hat j - 8\hat k} \right|\]
Using magnitude formula of vectors we get
\[
  \left| {6\hat i + 5\hat j - 8\hat k} \right| = \sqrt {{6^2} + {5^2} + {{( - 8)}^2}} \\
   = \sqrt {36 + 25 + 64} \\
   = \sqrt {125} \\
 \]
Now let us substitute the value of \[\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right|\]in the area of triangles formula, then we get,
The area of the triangle ABC
\[
  \dfrac{1}{2}\left| {\overrightarrow {AB} \times \overrightarrow {BC} } \right| \\
   = \dfrac{{\sqrt {125} }}{2}units \\
 \]

Hence no option in the given question matches the values, therefore we can convey that none of the given options are correct.

Note:
The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a × b.
\[(a \times b)\] and the name cross product were possibly inspired by the fact that each scalar component of $a \times b$ is computed by multiplying non-corresponding components of a and b.
The standard basis vectors $i,j{\text{ and }}k$ satisfy the following equalities in a right hand coordinate system:
$
  i \times j = k \\
  j \times k = i \\
  k \times i = j \\
 $
By the anticommutativity of the cross product,
$
  j \times i = - k \\
  k \times j = - i \\
  i \times k = - j \\
 $
Again by the anticommutativity of the cross product,
$
  i \times i = 0 \\
  j \times j = 0 \\
  k \times k = 0 \\
 $
We make mistakes in finding the cross product value of the given two vectors.