Question

If tangent drawn to a curve at a point is perpendicular to x-axis then at that point-
A. $ \dfrac{{dy}}{{dx}} = 0 $
B. $ \dfrac{{dx}}{{dy}} = 0 $
C. $ \dfrac{{dy}}{{dx}} = 1 $
D. $ \dfrac{{dy}}{{dx}} = - 1 $

Answer 1

Hint: A tangent line to a curve at a certain point is a line that touches the curve only at one point. Given that a tangent line drawn to a curve at a point is perpendicular to the x-axis. When a line is perpendicular to x-axis, it will be parallel to the y-axis. So, the x-coordinates of the line will not change only the y-coordinates will be changing. Use this info to solve the given question.

Complete step-by-step answer:
We are given that a tangent which is drawn to a curve at a point is perpendicular to x-axis.

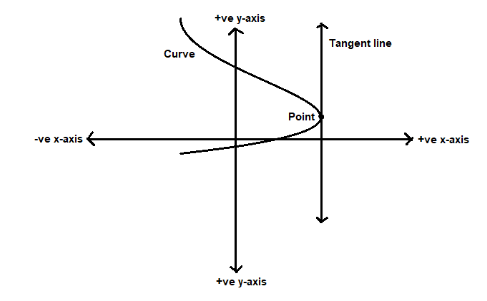
We know that when a line is perpendicular to x-axis, it is parallel to y-axis and when a line is perpendicular to y-axis then it is parallel to x-axis.
We know that the slope of a line m is equal to $ m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} $ , where $ {x_1},{x_2} $ are the x-coordinates of the points of a line and $ {y_1},{y_2} $ are the y-coordinates of the points of the line.
Slope can also be written as $ m = \dfrac{{dx}}{{dy}} $ , where $ dx $ is the change in x-coordinates and $ dy $ is the change in y-coordinates.
But the tangent line is parallel to the y-axis, just its y-coordinates will be changing keeping the x-coordinates constant.
Therefore,
  $
  dx = 0 \\
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{dy}}{0} \\
   \Rightarrow \dfrac{{dx}}{{dy}} = \dfrac{0}{{dy}} \\
  \therefore \dfrac{{dx}}{{dy}} = 0 \\
  $
So, the correct option is Option B, $ \dfrac{{dx}}{{dy}} = 0 $

So, the correct answer is “Option B”.

Note: Another approach
Straight line equation with slope m is $ y = mx + c $
Differentiate the line equation with respect to x
 $
  y = mx + c \\
  \dfrac{{dy}}{{dx}} = m\dfrac{{dx}}{{dx}} + \dfrac{d}{{dx}}c \\
  $
c is a constant, so its differentiation will be zero.
 $
  \dfrac{{dy}}{{dx}} = m\left( 1 \right) + 0\left( {\because \dfrac{{dx}}{{dx}} = 1} \right) \\
   \Rightarrow \dfrac{{dy}}{{dx}} = m \\
  $
But for a line which is perpendicular to the x-axis the slope is infinity.
 $
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{1}{0} \\
   \Rightarrow \dfrac{{dx}}{{dy}} = 0 \\
  $
Therefore, if tangent drawn to a curve at a point is perpendicular to x-axis then at that point $\dfrac{{dx}}{{dy}} = 0$