Answer
411.6k+ views
Hint:First of all, examine the quadrant of \[\theta \] and \[\phi \] by the given values of \[\sin \theta \] and \[\tan \phi \] respectively. Then find the sign of \[\tan \theta \] and \[\sec \phi \] in the respective quadrants. Now, find \[\tan \theta \] by first finding \[\cos \theta \] by using \[\sqrt{1-{{\sin }^{2}}\theta }\] and then taking the ratio \[\dfrac{\sin \theta }{\cos \theta }\]. Find \[\sec \phi \] by using \[\sqrt{1+{{\tan }^{2}}\phi }\] and then find the value of the desired expression.
Complete step-by-step answer:
In this question, we are given that \[\sin \theta =\dfrac{3}{5}\], \[\tan \phi =\dfrac{1}{2}\] and \[\dfrac{\pi }{2}<\theta <\phi <\dfrac{3\pi }{2}\]. Now, we have to find the value \[8\tan \theta -\sqrt{5}\sec \phi \]. Before proceeding with this question, let us see the sign of different trigonometric ratios in different quadrants. We have 6 trigonometric ratios and that are \[\sin \theta ,\cos \theta ,\tan \theta ,\cot \theta ,\operatorname{cosec}\theta \] and \[\sec \theta \].
1. In the first quadrant, that is from 0 to \[{{90}^{o}}\] or 0 to \[\dfrac{\pi }{2}\], all the trigonometric ratios are positive.
2. In the second quadrant, that is from \[{{90}^{o}}\] to \[{{180}^{o}}\] or \[\dfrac{\pi }{2}\] to \[\pi \], only \[\sin \theta \] and \[\operatorname{cosec}\theta \] are positive.
3. In the third quadrant, that is from \[{{180}^{o}}\] to \[{{270}^{o}}\] or \[\pi \] to \[\dfrac{3\pi }{2}\], only \[\tan \theta \] and \[\cot \theta \] are positive.
4. In the fourth quadrant, that is from \[{{270}^{o}}\] to \[{{360}^{o}}\] or \[\dfrac{3\pi }{2}\] to \[2\pi \], only \[\cos \theta \] and \[\sec \theta \] are positive.
This cycle would repeat after \[{{360}^{o}}\].
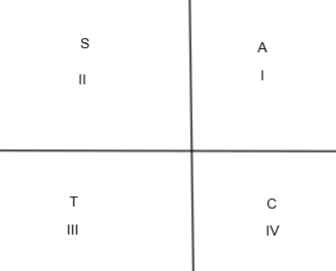
In this figure, A means all are positive, S means \[\sin \theta \] and \[\operatorname{cosec}\theta \] are positive, T means \[\tan \theta \] and \[\cot \theta \] are positive and C means \[\cos \theta \] and \[\sec \theta \] are positive.
Now, we are given that \[\theta \] is between \[\dfrac{\pi }{2}\] to \[\dfrac{3\pi }{2}\]. So \[\theta \] could be either in the second quadrant or third quadrant. But we are given that \[\sin \theta =\dfrac{3}{5}\] and out of the second quadrant and third quadrant, we know that \[\sin \theta \] is positive in the second quadrant only. So, from this, we have got that \[\theta \] is in the second quadrant that is between \[\dfrac{\pi }{2}\] to \[\pi \]. Also, in the second quadrant, all the trigonometric ratios except \[\sin \theta \] and \[\operatorname{cosec}\theta \] are negative. Now, \[\sin \theta =\dfrac{3}{5}\].
Now, we know that \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\] or \[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]. By substituting \[\sin \theta =\dfrac{3}{5}\], we get,
\[{{\cos }^{2}}\theta =1-{{\left( \dfrac{3}{5} \right)}^{2}}\]
\[{{\cos }^{2}}\theta =1-\dfrac{9}{25}\]
\[{{\cos }^{2}}\theta =\dfrac{16}{25}\]
\[\cos \theta =\sqrt{\dfrac{16}{25}}\]
\[\cos \theta =\pm \dfrac{4}{5}\]
We know that in the second quadrant, \[\cos \theta \] is negative. So, \[\cos \theta =\dfrac{-4}{5}\].
We also know that \[\tan \theta =\dfrac{\sin \theta }{\cos \theta }\]
So, by substituting the value of \[\sin \theta =\dfrac{3}{5}\] and \[\cos \theta =\dfrac{-4}{5}\]. We get,
\[\tan \theta =\dfrac{\left( \dfrac{3}{5} \right)}{\left( \dfrac{-4}{5} \right)}\]
\[\tan \theta =\left( \dfrac{3}{5} \right).\left( \dfrac{-5}{4} \right)\]
\[\tan \theta =\dfrac{-3}{4}\]
By multiplying 8 on both sides of the above equation, we get,
\[8\tan \theta =8\times \left( \dfrac{-3}{4} \right)\]
\[8\tan \theta =-6.....\left( i \right)\]
Now, we are also given that \[\phi \] is between \[\dfrac{\pi }{2}\] and \[\dfrac{3\pi }{2}\]. So \[\phi \] could be either in the second quadrant or third quadrant. But we are given that \[\tan \phi =\dfrac{1}{2}\] and out of the second and third quadrant, we know that \[\tan \phi \] is positive in the third quadrant only. So from this, we have got that \[\phi \] is in the third quadrant that is between \[\pi \] to \[\dfrac{3\pi }{2}\]. Also, in the third quadrant, all trigonometric ratios except \[\tan \theta \] and \[\cot \theta \] are negative.
Now, \[\tan \phi =\dfrac{1}{2}\]
We know that, \[{{\sec }^{2}}\phi =1+{{\tan }^{2}}\phi \]. So by substituting \[\tan \phi =\dfrac{1}{2}\], we get,
\[{{\sec }^{2}}\phi =1+{{\left( \dfrac{1}{2} \right)}^{2}}\]
\[{{\sec }^{2}}\phi =1+\dfrac{1}{4}\]
\[{{\sec }^{2}}\phi =\dfrac{5}{4}\]
\[\sec \phi =\pm \sqrt{\dfrac{5}{4}}\]
\[\sec \phi =\pm \dfrac{\sqrt{5}}{2}\]
We know that in the third quadrant, \[\sec \phi \] is negative, so we get, \[\sec \phi =\dfrac{-\sqrt{5}}{2}\]
By multiplying \[\left( -\sqrt{5} \right)\] on both sides of the above equation, we get,
\[-\sqrt{5}\sec \phi =\left( -\sqrt{5} \right)\left( \dfrac{-\sqrt{5}}{2} \right)\]
\[-\sqrt{5}\sec \phi =\dfrac{5}{2}.....\left( ii \right)\]
Now, by adding equation (i) and (ii), we get,
\[8\tan \theta -\sqrt{5}\sec \phi =\dfrac{-6}{1}+\dfrac{5}{2}\]
\[8\tan \theta -\sqrt{5}\sec \phi =\dfrac{-12+5}{2}=\dfrac{-7}{2}\]
So, we get the value of \[8\tan \theta -\sqrt{5}\sec \phi \] as \[\dfrac{-7}{2}\].
Note: In this question, many students make this mistake of taking \[\tan \theta \] and \[\sec \phi \] positive because \[\sin \theta \] and \[\tan \phi \] are also given positive which is wrong. In these questions, students must always try to locate the angle in one single quadrant to find the sign of all other trigonometric ratios as we did in the above solution to get the desired value. Also, students should find the angles carefully, they should not interchange \[\theta \] and \[\phi \].Students should remember the important trigonometric identities,formulas and standard angles to solve these types of questions.
Complete step-by-step answer:
In this question, we are given that \[\sin \theta =\dfrac{3}{5}\], \[\tan \phi =\dfrac{1}{2}\] and \[\dfrac{\pi }{2}<\theta <\phi <\dfrac{3\pi }{2}\]. Now, we have to find the value \[8\tan \theta -\sqrt{5}\sec \phi \]. Before proceeding with this question, let us see the sign of different trigonometric ratios in different quadrants. We have 6 trigonometric ratios and that are \[\sin \theta ,\cos \theta ,\tan \theta ,\cot \theta ,\operatorname{cosec}\theta \] and \[\sec \theta \].
1. In the first quadrant, that is from 0 to \[{{90}^{o}}\] or 0 to \[\dfrac{\pi }{2}\], all the trigonometric ratios are positive.
2. In the second quadrant, that is from \[{{90}^{o}}\] to \[{{180}^{o}}\] or \[\dfrac{\pi }{2}\] to \[\pi \], only \[\sin \theta \] and \[\operatorname{cosec}\theta \] are positive.
3. In the third quadrant, that is from \[{{180}^{o}}\] to \[{{270}^{o}}\] or \[\pi \] to \[\dfrac{3\pi }{2}\], only \[\tan \theta \] and \[\cot \theta \] are positive.
4. In the fourth quadrant, that is from \[{{270}^{o}}\] to \[{{360}^{o}}\] or \[\dfrac{3\pi }{2}\] to \[2\pi \], only \[\cos \theta \] and \[\sec \theta \] are positive.
This cycle would repeat after \[{{360}^{o}}\].

In this figure, A means all are positive, S means \[\sin \theta \] and \[\operatorname{cosec}\theta \] are positive, T means \[\tan \theta \] and \[\cot \theta \] are positive and C means \[\cos \theta \] and \[\sec \theta \] are positive.
Now, we are given that \[\theta \] is between \[\dfrac{\pi }{2}\] to \[\dfrac{3\pi }{2}\]. So \[\theta \] could be either in the second quadrant or third quadrant. But we are given that \[\sin \theta =\dfrac{3}{5}\] and out of the second quadrant and third quadrant, we know that \[\sin \theta \] is positive in the second quadrant only. So, from this, we have got that \[\theta \] is in the second quadrant that is between \[\dfrac{\pi }{2}\] to \[\pi \]. Also, in the second quadrant, all the trigonometric ratios except \[\sin \theta \] and \[\operatorname{cosec}\theta \] are negative. Now, \[\sin \theta =\dfrac{3}{5}\].
Now, we know that \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\] or \[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]. By substituting \[\sin \theta =\dfrac{3}{5}\], we get,
\[{{\cos }^{2}}\theta =1-{{\left( \dfrac{3}{5} \right)}^{2}}\]
\[{{\cos }^{2}}\theta =1-\dfrac{9}{25}\]
\[{{\cos }^{2}}\theta =\dfrac{16}{25}\]
\[\cos \theta =\sqrt{\dfrac{16}{25}}\]
\[\cos \theta =\pm \dfrac{4}{5}\]
We know that in the second quadrant, \[\cos \theta \] is negative. So, \[\cos \theta =\dfrac{-4}{5}\].
We also know that \[\tan \theta =\dfrac{\sin \theta }{\cos \theta }\]
So, by substituting the value of \[\sin \theta =\dfrac{3}{5}\] and \[\cos \theta =\dfrac{-4}{5}\]. We get,
\[\tan \theta =\dfrac{\left( \dfrac{3}{5} \right)}{\left( \dfrac{-4}{5} \right)}\]
\[\tan \theta =\left( \dfrac{3}{5} \right).\left( \dfrac{-5}{4} \right)\]
\[\tan \theta =\dfrac{-3}{4}\]
By multiplying 8 on both sides of the above equation, we get,
\[8\tan \theta =8\times \left( \dfrac{-3}{4} \right)\]
\[8\tan \theta =-6.....\left( i \right)\]
Now, we are also given that \[\phi \] is between \[\dfrac{\pi }{2}\] and \[\dfrac{3\pi }{2}\]. So \[\phi \] could be either in the second quadrant or third quadrant. But we are given that \[\tan \phi =\dfrac{1}{2}\] and out of the second and third quadrant, we know that \[\tan \phi \] is positive in the third quadrant only. So from this, we have got that \[\phi \] is in the third quadrant that is between \[\pi \] to \[\dfrac{3\pi }{2}\]. Also, in the third quadrant, all trigonometric ratios except \[\tan \theta \] and \[\cot \theta \] are negative.
Now, \[\tan \phi =\dfrac{1}{2}\]
We know that, \[{{\sec }^{2}}\phi =1+{{\tan }^{2}}\phi \]. So by substituting \[\tan \phi =\dfrac{1}{2}\], we get,
\[{{\sec }^{2}}\phi =1+{{\left( \dfrac{1}{2} \right)}^{2}}\]
\[{{\sec }^{2}}\phi =1+\dfrac{1}{4}\]
\[{{\sec }^{2}}\phi =\dfrac{5}{4}\]
\[\sec \phi =\pm \sqrt{\dfrac{5}{4}}\]
\[\sec \phi =\pm \dfrac{\sqrt{5}}{2}\]
We know that in the third quadrant, \[\sec \phi \] is negative, so we get, \[\sec \phi =\dfrac{-\sqrt{5}}{2}\]
By multiplying \[\left( -\sqrt{5} \right)\] on both sides of the above equation, we get,
\[-\sqrt{5}\sec \phi =\left( -\sqrt{5} \right)\left( \dfrac{-\sqrt{5}}{2} \right)\]
\[-\sqrt{5}\sec \phi =\dfrac{5}{2}.....\left( ii \right)\]
Now, by adding equation (i) and (ii), we get,
\[8\tan \theta -\sqrt{5}\sec \phi =\dfrac{-6}{1}+\dfrac{5}{2}\]
\[8\tan \theta -\sqrt{5}\sec \phi =\dfrac{-12+5}{2}=\dfrac{-7}{2}\]
So, we get the value of \[8\tan \theta -\sqrt{5}\sec \phi \] as \[\dfrac{-7}{2}\].
Note: In this question, many students make this mistake of taking \[\tan \theta \] and \[\sec \phi \] positive because \[\sin \theta \] and \[\tan \phi \] are also given positive which is wrong. In these questions, students must always try to locate the angle in one single quadrant to find the sign of all other trigonometric ratios as we did in the above solution to get the desired value. Also, students should find the angles carefully, they should not interchange \[\theta \] and \[\phi \].Students should remember the important trigonometric identities,formulas and standard angles to solve these types of questions.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Assertion The resistivity of a semiconductor increases class 13 physics CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the stopping potential when the metal with class 12 physics JEE_Main

The momentum of a photon is 2 times 10 16gm cmsec Its class 12 physics JEE_Main

Using the following information to help you answer class 12 chemistry CBSE

Trending doubts
Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How fast is 60 miles per hour in kilometres per ho class 10 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

How do you solve x2 11x + 28 0 using the quadratic class 10 maths CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Which are the major cities located on the river Ga class 10 social science CBSE

What is BLO What is the full form of BLO class 8 social science CBSE



