Question

If PQ be a normal chord of the parabola and if S be the focus, prove that the locus of the centroid of the triangle SPQ is curve $36a{y^2}\left( {3x - 5a} \right) - 81{y^4} = 128{a^4}$.

Answer 1

Hint- Always remember the equation of the normal chord. And put the values as ${t_1},{t_2}$. We will solve the question by using the formula of the centroid of a triangle SPQ given the coordinates are $\left( {h,k} \right)$. The formula will be $h = \dfrac{{a + at_1^2 + a{{\left( {{t_1} + {{\dfrac{2}{t}}_1}} \right)}^2}}}{3}$, $k = \dfrac{{0 + 2a{t_1} - 2a{t_1} - \dfrac{{4a}}{{{t_1}}}}}{3}$

Complete Step-by-step answer:

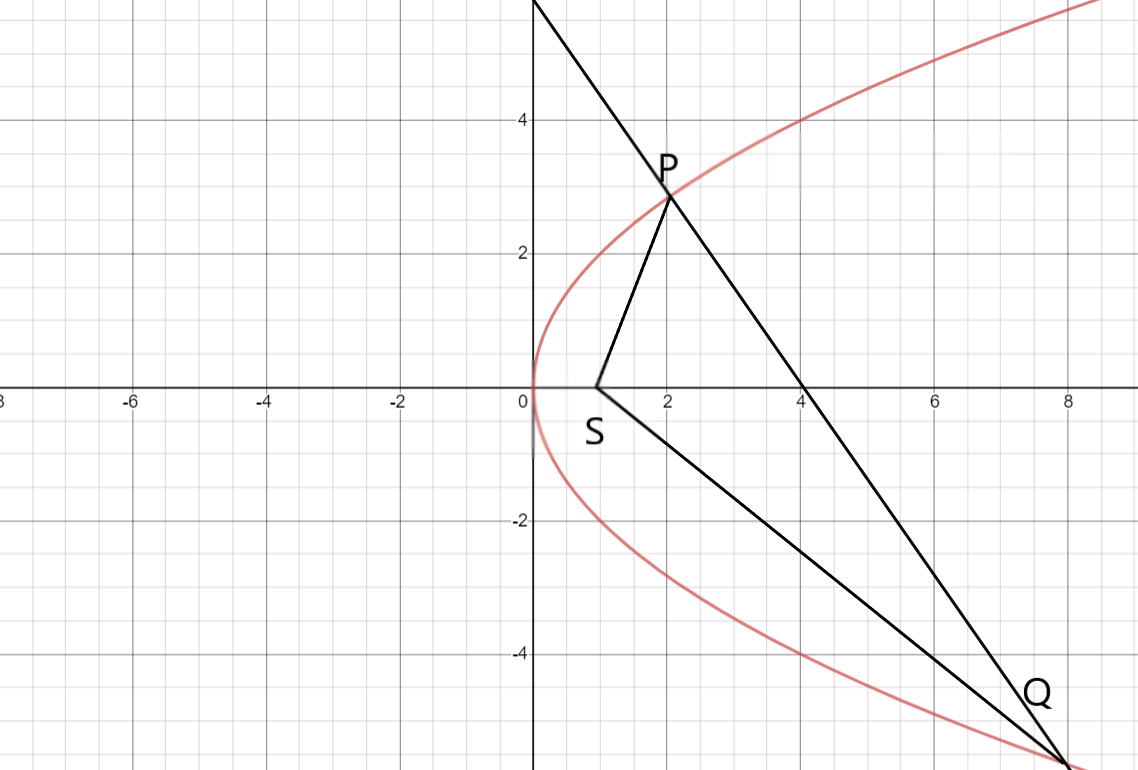
If the focus of the parabola is S, then the coordinates will be $\left( {a,0} \right)$.
As we all know, the equation of a parabola is ${y^2} = 4ax$.
Let the equation of the normal chord at point P be $P\left( {at_1^2,2a{t_1}} \right)$.
Then, the value of y will be-
$y = {t_1}x - 2a{t_1} - at_1^3$
Let the other point where it cuts be named Q, then the coordinates of the point Q will be $Q\left( {at_2^2,2a{t_2}} \right)$.
The relation here is-
${t_2} = - {t_1} - \dfrac{2}{{{t_1}}}$
The formula for the centroid of the triangle SPQ where the coordinates are $\left( {h,k} \right)$is:
 $h = \dfrac{{a + at_1^2 + a{{\left( {{t_1} + {{\dfrac{2}{t}}_1}} \right)}^2}}}{3}$
$k = \dfrac{{0 + 2a{t_1} - 2a{t_1} - \dfrac{{4a}}{{{t_1}}}}}{3}$
$ \Rightarrow {t_1} = \dfrac{{ - 4a}}{{3k}}$
Now, as we know,
$h = \dfrac{{3a + 2at_1^2 + \dfrac{{4a}}{{t_1^2}}}}{3}$
So,
$3h = 3a + 2a{\left( {\dfrac{{ - 4a}}{{3k}}} \right)^2} + \dfrac{{4a}}{{{{\left( {\dfrac{{ - 4a}}{{3k}}} \right)}^2}}}$
Replacing $\left( {h,k} \right)$ by $\left( {x,y} \right)$, we get this:
$36a{y^2}\left( {3x - 5a} \right) - 81{y^4} = 128{a^4}$
Hence proved.

Note: Use the equation of parabola in the starting of the question and pay special attention to the superscripts and subscripts as they are a wee but congested in these type of questions and mat completely vary your answer if not done in a right way.