Question

If \[P\left( {{t}^{2}},2t \right)\], \[t\in [0,2]\], is an arbitrary point on the parabola \[{{y}^{2}}=4x\], Q is the foot of the perpendicular from the focus S on the tangent at P, then maximum area of $\Delta $ PQS is
(a) 1
(b) 2
(c) \[\dfrac{5}{16}\]
(d) 5

Answer 1

Hint: We will first find the tangent equation and then find the foot of the perpendicular on it. So we have all the three points and they form a right angled triangle as they mentioned “perpendicular”. So we can find the height and the length of the base. Finally we will just apply the \[\dfrac{1}{2}bh\] formula and get the area. Then we will see its behavior in the interval [0, 2] and find its maximum.

Complete step-by-step answer:
First let us have a look at the diagram.

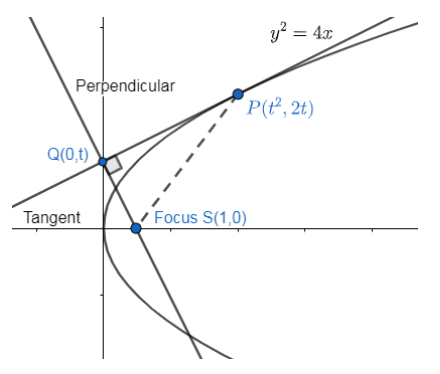
Now we know the point\[P\left( {{t}^{2}},2t \right)\]. Let us find the equation of the tangent at that point.
Let the equation of the tangent be \[y=mx+c\].
Now let us find the slope m.
Given equation of the curve is,
\[{{y}^{2}}=4x\]
\[\Rightarrow {{y}^{2}}-4x=0\]
Differentiating with respect to x on both sides we get,
\[\begin{align}
  & 2y\dfrac{dy}{dx}-4=0 \\
 & \Rightarrow 2y\dfrac{dy}{dx}=4 \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{4}{2y} \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{2}{y} \\
 & \Rightarrow m=\dfrac{2}{y} \\
\end{align}\]
Since \[\dfrac{dy}{dx}\] is slope m.
Now let us substitute the point \[P\left( {{t}^{2}},2t \right)\] in the above equation. Therefore,
\[\begin{align}
  & m=\dfrac{2}{2t} \\
 & \Rightarrow m=\dfrac{1}{t} \\
\end{align}\]
Thus, the equation of the tangent becomes,
\[y=\dfrac{1}{t}x+c\]
Now to find the constant c, substitute the point \[P\left( {{t}^{2}},2t \right)\] in the equation of the tangent since the tangent passes through that point. Therefore, we get,
\[\begin{align}
  & 2t=\dfrac{1}{t}{{t}^{2}}+c \\
 & \Rightarrow 2t=t+c \\
 & \Rightarrow t=c \\
\end{align}\]
Thus the equation of the tangent on the given parabola at the point \[P\left( {{t}^{2}},2t \right)\] is,
 \[y=\dfrac{1}{t}x+t\]
\[\Rightarrow \dfrac{1}{t}x-y+t=0\]
Now let us find the foot of the perpendicular from focus S.
First, we need the co-ordinates of the focus S.
General form of the parabola is \[{{y}^{2}}=4ax\], where (a, 0) is its focus.
Comparing the given parabola with the general equation we get, \[a=1\].
Thus the co-ordinates of the focus are (1,0).
Thus, we need to find the foot of the perpendicular from S (1, 0) to the tangent. How do we do that?
First let us find the line perpendicular to the tangent and which is passing S (1, 0).
To find the perpendicular line we exchange the coefficients of the x and y terms and then let the constant be k. Thus the equation of the perpendicular is,
\[x+\dfrac{1}{t}y=k\].
Now it passes through the point (1, 0), substituting the point (1,0) in the equation we get,
\[\begin{align}
  & 1+0=k \\
 & \Rightarrow k=1 \\
\end{align}\]
Therefore, the equation of the perpendicular becomes,
\[x+\dfrac{1}{t}y=1\]
Solving this line equation and the tangent equation, we get the foot of the perpendicular from S (1, 0). Solving these two,
\[\begin{align}
  & \dfrac{1}{t}x-y+t=0..........\times t \\
 & x+\dfrac{1}{t}y-1=0..........\times 1 \\
\end{align}\]
This gives us,
\[\begin{align}
  & x-ty+{{t}^{2}}=0 \\
 & x+\dfrac{1}{t}y-1=0 \\
\end{align}\]
Subtracting the like terms we get,
\[\begin{align}
  & \left( -t-\dfrac{1}{t} \right)y+({{t}^{2}}+1)=0 \\
 & \Rightarrow ({{t}^{2}}+1)=\left( t+\dfrac{1}{t} \right)y \\
 & \Rightarrow ({{t}^{2}}+1)=\left( \dfrac{{{t}^{2}}+1}{t} \right)y \\
\end{align}\]
Cancelling the like terms and cross-multiplying we get,
y = t
Now substituting y = t in the tangent equation we get the x co-ordinate.
\[\dfrac{1}{t}x-y+t=0\]
\[\begin{align}
  & \Rightarrow \dfrac{1}{t}x-t+t=0 \\
 & \Rightarrow \dfrac{1}{t}x=0 \\
 & \Rightarrow x=0 \\
\end{align}\]
Thus, the foot of the perpendicular has co-ordinates Q (0, t).
Thus, we know the co-ordinates \[P\left( {{t}^{2}},\text{ }2t \right),\text{ }Q\left( 0,\text{ }t \right)\] and S (1, 0) and these form a right angled triangle as there is a “perpendicular” line.
The right angle is that the foot of the perpendicular that is Q.
Now let us find the distance between the points P and Q and then between the points Q and S. Now,
\[\begin{align}
  & PQ=\sqrt{{{\left( {{x}_{P}}-{{x}_{Q}} \right)}^{2}}+{{\left( {{y}_{P}}-{{y}_{Q}} \right)}^{2}}} \\
 & \Rightarrow PQ=\sqrt{{{\left( {{t}^{2}}-0 \right)}^{2}}+{{\left( 2t-t \right)}^{2}}} \\
 & \Rightarrow PQ=\sqrt{{{t}^{4}}+{{t}^{2}}} \\
 & \Rightarrow PQ=t\sqrt{{{t}^{2}}+1} \\
\end{align}\]
Similarly,
\[\begin{align}
  & SQ=\sqrt{{{\left( {{x}_{S}}-{{x}_{Q}} \right)}^{2}}+{{\left( {{y}_{S}}-{{y}_{Q}} \right)}^{2}}} \\
 & \Rightarrow SQ=\sqrt{{{\left( 1-0 \right)}^{2}}+{{\left( 0-t \right)}^{2}}} \\
 & \Rightarrow SQ=\sqrt{1+{{t}^{2}}} \\
 & \Rightarrow SQ=\sqrt{{{t}^{2}}+1} \\
\end{align}\]
Now PQ becomes the base and SQ becomes the height. Thus,
\[\begin{align}
  & Area=\dfrac{1}{2}PQ\times SQ \\
 & \Rightarrow Area=\dfrac{1}{2}t\sqrt{{{t}^{2}}+1}\times \sqrt{{{t}^{2}}+1} \\
 & \Rightarrow Area=\dfrac{1}{2}t\left( {{t}^{2}}+1 \right) \\
 & \Rightarrow Area=\dfrac{{{t}^{3}}+t}{2} \\
\end{align}\]
Now as t ϵ [0, 2], Area becomes maximum at t = 2 because \[{{t}^{3}}+t\] would be increasing in that interval.

Thus putting t =2 in the area equation we get,
\[\begin{align}
  & Area=\dfrac{2+{{2}^{3}}}{2} \\
 & \Rightarrow Area=\dfrac{2+8}{2} \\
 & \Rightarrow Area=\dfrac{10}{2} \\
 & \Rightarrow Area=5 \\
\end{align}\]
Thus option(d) is correct.

Note:There is a shortcut for finding the foot of the perpendicular.
Let the co-ordinates of the foot of the perpendicular be (h, k) from the point (p,q) on the line \[ax+by+c=0\]. The formula is,
\[\dfrac{h-p}{a}\text{ }=\text{ }\dfrac{k-q}{b}\text{ }=\dfrac{-\left( ap+bq+c \right)}{({{a}^{2}}+{{b}^{2}})}\]
This formula will save you a lot of time.