Question

If one of the angles of triangle is $ {130^o} $ ,then the angle between the bisectors of the other two angles can be:
A.\[{50^o}\]
B. $ {65^o} $
C. $ {145^o} $
D. $ {155^o} $

Answer 1

Hint: In order to solve this question we will apply the concept of sum of angles of triangle so the concept of sum of triangles is that the sum of angles of triangle is equal to $ {180^o} $ . Then we will consider the angle bisectors and we will find the complete bisectors of these two angles then we will again use the concept of the sum of angles of the triangle and find the resultant.

Complete step by step solution:
For solving this question we will first find the triangle ABC as shown in the below figure.

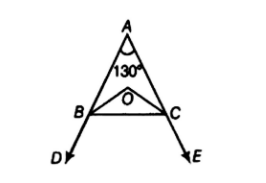
Let the given angle b $ \angle BAC $ and also let the angle bisector of angle B and C meets at O and we have to find angle BOC, hence we will find the remaining angles of triangle in combined form so the remaining angles of triangle will be:
 $ \angle BAC + \angle ABC + \angle CBA = {180^o} $
Now as it is given to us the one angle of triangle so we will find the remaining angles in combined form:
 $ \angle ABC + \angle BCA = {50^o} $
Since it is given to us that we have to find the angle bisectors so we will make all the angles to half of it so we will do as:
 $ \dfrac{1}{2}(\angle ABC + \angle BCA) = {25^o} $
Now we will again use the concept of sum of angles of triangle in triangle OBC:
 $ \angle OBC + \angle OCB + \angle BOC = {180^o} $
Since the bisectors might be equal to the angles unknown in this equation so we will find the BOC:
 $ \angle BOC + {25^o} = {180^o} $
Now on substituting all the values to other side we will get the value of:
 $ \angle BOC = {155^o} $
So the correct option will be D.
So, the correct answer is “Option D”.

Note: For solving these types question we should keep in mind that we will have to assume the angle bisector it is not the appropriate value of the angle BOC since we are not the appropriate value of the angle bisectors as these values can be of the given angle bisector.