Question

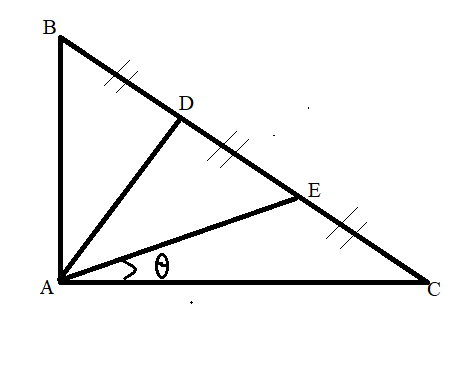
If in a triangle ABC, BC=5, CA=4, AB=3 and D, E are points on BC such that BD=DE=EC, ∠CAE=θ.
This question has multiple correct options
A. ${\text{A}}{{\text{E}}^2} = \dfrac{{73}}{3}$
B. ${\text{A}}{{\text{E}}^2} = \dfrac{{73}}{9}$
C. ${\text{tan}}\theta {\text{ = }}\dfrac{3}{8}$
D. ​$\cos \theta = 3\sqrt {73} $

Answer 1

Hint: Proceed the solution of this question, first by finding the relationship between the sides and their length so that by putting the values of length of sides of triangles in SOLUTION OF TRIANGLE formulas we can reach our answers.

Complete step-by-step solution -
In the question it is given that BC=5, CA=4, AB=3 and BD=DE=EC, ∠CAE=θ.
BC=BD+DE+EC =5
$\because $BD=DE=EC
$\therefore $ BD=DE=EC =$\dfrac{5}{3}$​ and triangle ABC is a right angled triangle.

We know that,
$\cos {\text{C = }}\dfrac{{{{\text{a}}^2} + {{\text{b}}^2} - {{\text{c}}^2}}}{{2{\text{ab}}}}$ , where a, b, c are the sides of triangle angle $∠A, ∠B, ∠C $ are the angles opposite of side AB, BC and CA
So here, Apply SOT formula in this triangle AEC,
So a = EC, b = AC and c = AE
$\cos {\text{C = }}\dfrac{{{\text{E}}{{\text{C}}^2} + {\text{A}}{{\text{C}}^2}{\text{ - A}}{{\text{E}}^2}}}{{2{\text{EC}}.{\text{AC}}}}$


On Cross Multiplication
$\cos {\text{C}} \times 2{\text{EC}}.{\text{AC = E}}{{\text{C}}^2} + {\text{A}}{{\text{C}}^2}{\text{ - A}}{{\text{E}}^2}$
${\text{A}}{{\text{E}}^2}{\text{ = E}}{{\text{C}}^2} + {\text{A}}{{\text{C}}^2}{\text{ - }}\cos {\text{C}} \times 2{\text{EC}}.{\text{AC}}$
${\text{A}}{{\text{E}}^2}{\text{ = }}{\left( {\dfrac{5}{3}} \right)^2} + {{\text{4}}^2}{\text{ - }}\cos {\text{C}} \times 2\dfrac{5}{3} \times 4$
${\text{A}}{{\text{E}}^2}{\text{ = }}\dfrac{{25}}{9} + 16{\text{ - }}\cos {\text{C}} \times \dfrac{{40}}{3}$
From Δ ABC, we know that

$\cos {\text{C = }}\dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{4}{5}$
${\text{A}}{{\text{E}}^2}{\text{ = }}\dfrac{{25}}{9} + 16{\text{ - }}\dfrac{4}{5} \times \dfrac{{40}}{3}$
${\text{A}}{{\text{E}}^2}{\text{ = }}\dfrac{{25}}{9} + 16{\text{ - }}\dfrac{4}{1} \times \dfrac{8}{3}$
${\text{A}}{{\text{E}}^2}{\text{ = }}\dfrac{{25}}{9} + 16{\text{ - }}\dfrac{4}{1} \times \dfrac{8}{3} = \dfrac{{25}}{9} + \dfrac{{16}}{1} - \dfrac{{32}}{3} = \dfrac{{25 + 144 - 96}}{9} = \dfrac{{73}}{9}$
${\text{A}}{{\text{E}}^2} = \dfrac{{73}}{9}$………. Hence option B is correct
On taking square root on both sides
${\text{AE}} = \sqrt {\dfrac{{73}}{9}} = \dfrac{{\sqrt {73} }}{3}$

$\cos \theta {\text{ = }}\dfrac{{{\text{A}}{{\text{E}}^2} + {\text{A}}{{\text{C}}^2}{\text{ - E}}{{\text{C}}^2}}}{{2{\text{AE}}.{\text{EC}}}}$
On putting all the values
$\cos \theta {\text{ = }}\dfrac{{\dfrac{{73}}{9} + {{\text{4}}^2}{\text{ - }}{{\left( {\dfrac{5}{3}} \right)}^2}}}{{2\sqrt {\dfrac{{73}}{9}} .{\text{4}}}} = \dfrac{{\dfrac{{73 + 144 - 25}}{9}}}{{\dfrac{{\sqrt {73} }}{3} \times 8}} = \dfrac{{192}}{{\sqrt {73} \times 24}} = \dfrac{8}{{\sqrt {73} }}$
Hence $\sec \theta {\text{ = }}\dfrac{{\sqrt {73} }}{8}$

Now, we know that
$ \Rightarrow \tan \theta = \sqrt {{\text{se}}{{\text{c}}^2}\theta - 1} $
On putting value of ${\text{sec}}\theta $
$ \Rightarrow \tan \theta = \sqrt {{{\left( {\dfrac{{\sqrt {73} }}{8}} \right)}^2} - 1} $
$ \Rightarrow \tan \theta = \sqrt {\dfrac{{73}}{{64}} - 1} $
$ \Rightarrow \tan \theta = \sqrt {\dfrac{9}{{64}}} $
$ \Rightarrow \tan \theta = \dfrac{3}{8}$

Note: To solve this particular concept we should have a good grasp on trigonometric concepts such as

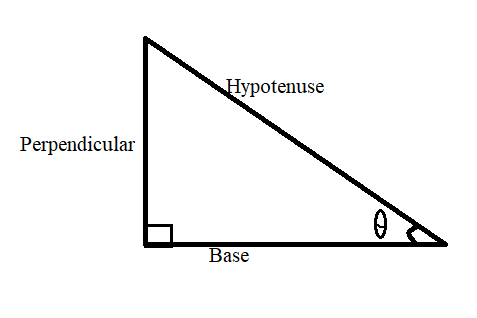
${\text{sin}}\theta {\text{ = }}\dfrac{{{\text{Perpendicular (or opposite side wrt }}\theta {\text{)}}}}{{{\text{Hypotenuse}}}}$,
$\cos \theta {\text{ = }}\dfrac{{{\text{Base (or Adjacent side wrt }}\theta {\text{)}}}}{{{\text{Hypotenuse}}}}$,
${\text{tan}}\theta {\text{ = }}\dfrac{{{\text{Perpendicular (or opposite side wrt }}\theta {\text{)}}}}{{{\text{Base}}}}$
Along with that we should have a good understanding of the Solution of triangle formula (SOT) and their use.