
if have a function as $f\left( x \right)=\cos \left[ 2\pi \right]x+\cos \left[ -2\pi \right]x$, where $\left[ x \right]$ stands for the greatest integer function, then This question has multiple correct options
A. $f\left( \dfrac{\pi }{2} \right)=-1$
B. $f\left( \pi \right)=+1$
C. $f\left( -\pi \right)=0$
D. $f\left( \dfrac{\pi }{4} \right)=1$
Answer
580.2k+ views
Hint: We will first calculate the values of $\left[ 2\pi \right],\left[ -2\pi \right]$ using the values of $\pi $ as $3.14$ and from the given data $\left[ x \right]$ stands for the greatest integer function. Now we will substitute those values in the given function. In the problem they mentioned that the question has multiple correct answers, so we will check each option for the obtained function.
Complete step-by-step solution
Given that,
$f\left( x \right)=\cos \left[ 2\pi \right]x+\cos \left[ -2\pi \right]x$
Substituting the value of $\pi =3.14$ to find the value of $\left[ 2\pi \right]$, then
$\begin{align}
& \left[ 2\pi \right]=\left[ 2\times 3.14 \right] \\
& =\left[ 6.28 \right]
\end{align}$
Given that $\left[ x \right]$stands for the greatest integer function, then greatest integer value of $6.28$ is $6$, hence the value of $\left[ 6.28 \right]$ is $6$. i.e.
$\left[ 2\pi \right]=6....\left( \text{i} \right)$
Substituting the value of $\pi =3.14$ to find the value of $\left[ -2\pi \right]$, then
$\begin{align}
& \left[ -2\pi \right]=\left[ -2\times 3.14 \right] \\
& =\left[ -6.28 \right]
\end{align}$
Given that $\left[ x \right]$stands for the greatest integer function, then greatest integer value of $-6.28$ is $-7$, hence the value of $\left[ -6.28 \right]$ is $-7$. i.e.
$\left[ -2\pi \right]=-7....\left( \text{ii} \right)$
From equations $\left( \text{i} \right)$ and $\left( \text{ii} \right)$, substituting the values of $\left[ 2\pi \right],\left[ -2\pi \right]$ in given function, then
$\begin{align}
& f\left( x \right)=\cos \left[ 2\pi \right]x+\cos \left[ -2\pi \right]x \\
& =\cos \left( 6 \right)x+\cos \left( -7 \right)x
\end{align}$
We know that $\cos \left( -\theta \right)=\cos \theta $, then
$f\left( x \right)=\cos 6x+\cos 7x$
Hence the simplified form of the given function is $f\left( x \right)=\cos 6x+\cos 7x$
The values of
$\begin{align}
& f\left( \dfrac{\pi }{2} \right)=\cos 6\left( \dfrac{\pi }{2} \right)+\cos 7\left( \dfrac{\pi }{2} \right) \\
& =\cos 3\pi +\cos \left( \dfrac{7\pi }{2} \right) \\
& =\cos \left( 2\pi +\pi \right)+\cos \left( 5\pi +\dfrac{\pi }{2} \right) \\
& =\cos \left( 2\pi +\pi \right)+\cos \left( 2\left( 2\pi \right)+\pi +\dfrac{\pi }{2} \right)
\end{align}$
We know that $\cos \left( 2n\pi +\theta \right)=\cos \theta $, where $n=1,2,3,4...$, then
$f\left( \dfrac{\pi }{2} \right)=\cos \pi +\cos \left( \dfrac{3\pi }{2} \right)$
We know that the values of $\cos \pi $ as $-1$ and $\cos \left( \dfrac{3\pi }{2} \right)$ as $0$, then
$\begin{align}
& f\left( \dfrac{\pi }{2} \right)=-1+0 \\
& f\left( \dfrac{\pi }{2} \right)=-1.....\left( \text{a} \right)
\end{align}$
Now the value of $f\left( \pi \right)$ is
$\begin{align}
& f\left( \pi \right)=\cos 6\pi +\cos 7\pi \\
& =\cos \left( 2\left( 3 \right)\pi \right)+\cos \left( 2\left( 3 \right)\pi +\pi \right)
\end{align}$
We know that $\cos \left( 2n\pi +\theta \right)=\cos \theta $ and $\cos \left( 2n\pi \right)=1$ for $n=1,2,3,4...$, then
$f\left( \pi \right)=1+\cos \pi $
We know that the value of $\cos \pi $ as $-1$, then
$\begin{align}
& f\left( \pi \right)=1-1 \\
& =0.....\left( \text{b} \right)
\end{align}$
Now the value of $f\left( -\pi \right)$ is
$f\left( -\pi \right)=\cos 6\left( -\pi \right)+\cos 7\left( -\pi \right)$
We know that $\cos \left( -\theta \right)=\cos \theta $, then
$\begin{align}
& f\left( -\pi \right)=\cos 6\pi +\cos 7\pi \\
& f\left( -\pi \right)=f\left( \pi \right) \\
& f\left( -\pi \right)=0....\left( \text{c} \right)
\end{align}$
Now the value of $f\left( \dfrac{\pi }{4} \right)$ is
$\begin{align}
& f\left( \dfrac{\pi }{4} \right)=\cos 6\left( \dfrac{\pi }{4} \right)+\cos 7\left( \dfrac{\pi }{4} \right) \\
& =\cos \left( \dfrac{3\pi }{2} \right)+\cos \left( \pi +\dfrac{3\pi }{4} \right)
\end{align}$
Substituting the values of $\cos \left( \dfrac{3\pi }{2} \right)=0$ and $\cos \left( \dfrac{7\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$ then
$\begin{align}
& f\left( \dfrac{\pi }{4} \right)=0+\dfrac{1}{\sqrt{2}} \\
& =\dfrac{1}{\sqrt{2}}.....\left( \text{d} \right)
\end{align}$
From the equations $\left( \text{a} \right),\left( \text{b} \right),\left( \text{c} \right),\left( \text{d} \right)$ we can say that options $\text{A,C}$ are the correct options.
Note: The students may make mistakes when they are taking the greatest integer of $-6.28$. The greatest Integer of $-6.28$ is $7$, don’t take it as $6$. If you take it as $6$, then the whole solution will be deflected from the correct way. You can also refer to the below picture to check the greatest integer values
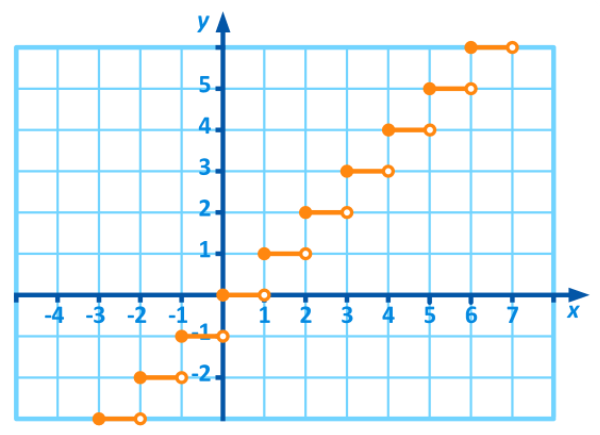
Complete step-by-step solution
Given that,
$f\left( x \right)=\cos \left[ 2\pi \right]x+\cos \left[ -2\pi \right]x$
Substituting the value of $\pi =3.14$ to find the value of $\left[ 2\pi \right]$, then
$\begin{align}
& \left[ 2\pi \right]=\left[ 2\times 3.14 \right] \\
& =\left[ 6.28 \right]
\end{align}$
Given that $\left[ x \right]$stands for the greatest integer function, then greatest integer value of $6.28$ is $6$, hence the value of $\left[ 6.28 \right]$ is $6$. i.e.
$\left[ 2\pi \right]=6....\left( \text{i} \right)$
Substituting the value of $\pi =3.14$ to find the value of $\left[ -2\pi \right]$, then
$\begin{align}
& \left[ -2\pi \right]=\left[ -2\times 3.14 \right] \\
& =\left[ -6.28 \right]
\end{align}$
Given that $\left[ x \right]$stands for the greatest integer function, then greatest integer value of $-6.28$ is $-7$, hence the value of $\left[ -6.28 \right]$ is $-7$. i.e.
$\left[ -2\pi \right]=-7....\left( \text{ii} \right)$
From equations $\left( \text{i} \right)$ and $\left( \text{ii} \right)$, substituting the values of $\left[ 2\pi \right],\left[ -2\pi \right]$ in given function, then
$\begin{align}
& f\left( x \right)=\cos \left[ 2\pi \right]x+\cos \left[ -2\pi \right]x \\
& =\cos \left( 6 \right)x+\cos \left( -7 \right)x
\end{align}$
We know that $\cos \left( -\theta \right)=\cos \theta $, then
$f\left( x \right)=\cos 6x+\cos 7x$
Hence the simplified form of the given function is $f\left( x \right)=\cos 6x+\cos 7x$
The values of
$\begin{align}
& f\left( \dfrac{\pi }{2} \right)=\cos 6\left( \dfrac{\pi }{2} \right)+\cos 7\left( \dfrac{\pi }{2} \right) \\
& =\cos 3\pi +\cos \left( \dfrac{7\pi }{2} \right) \\
& =\cos \left( 2\pi +\pi \right)+\cos \left( 5\pi +\dfrac{\pi }{2} \right) \\
& =\cos \left( 2\pi +\pi \right)+\cos \left( 2\left( 2\pi \right)+\pi +\dfrac{\pi }{2} \right)
\end{align}$
We know that $\cos \left( 2n\pi +\theta \right)=\cos \theta $, where $n=1,2,3,4...$, then
$f\left( \dfrac{\pi }{2} \right)=\cos \pi +\cos \left( \dfrac{3\pi }{2} \right)$
We know that the values of $\cos \pi $ as $-1$ and $\cos \left( \dfrac{3\pi }{2} \right)$ as $0$, then
$\begin{align}
& f\left( \dfrac{\pi }{2} \right)=-1+0 \\
& f\left( \dfrac{\pi }{2} \right)=-1.....\left( \text{a} \right)
\end{align}$
Now the value of $f\left( \pi \right)$ is
$\begin{align}
& f\left( \pi \right)=\cos 6\pi +\cos 7\pi \\
& =\cos \left( 2\left( 3 \right)\pi \right)+\cos \left( 2\left( 3 \right)\pi +\pi \right)
\end{align}$
We know that $\cos \left( 2n\pi +\theta \right)=\cos \theta $ and $\cos \left( 2n\pi \right)=1$ for $n=1,2,3,4...$, then
$f\left( \pi \right)=1+\cos \pi $
We know that the value of $\cos \pi $ as $-1$, then
$\begin{align}
& f\left( \pi \right)=1-1 \\
& =0.....\left( \text{b} \right)
\end{align}$
Now the value of $f\left( -\pi \right)$ is
$f\left( -\pi \right)=\cos 6\left( -\pi \right)+\cos 7\left( -\pi \right)$
We know that $\cos \left( -\theta \right)=\cos \theta $, then
$\begin{align}
& f\left( -\pi \right)=\cos 6\pi +\cos 7\pi \\
& f\left( -\pi \right)=f\left( \pi \right) \\
& f\left( -\pi \right)=0....\left( \text{c} \right)
\end{align}$
Now the value of $f\left( \dfrac{\pi }{4} \right)$ is
$\begin{align}
& f\left( \dfrac{\pi }{4} \right)=\cos 6\left( \dfrac{\pi }{4} \right)+\cos 7\left( \dfrac{\pi }{4} \right) \\
& =\cos \left( \dfrac{3\pi }{2} \right)+\cos \left( \pi +\dfrac{3\pi }{4} \right)
\end{align}$
Substituting the values of $\cos \left( \dfrac{3\pi }{2} \right)=0$ and $\cos \left( \dfrac{7\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$ then
$\begin{align}
& f\left( \dfrac{\pi }{4} \right)=0+\dfrac{1}{\sqrt{2}} \\
& =\dfrac{1}{\sqrt{2}}.....\left( \text{d} \right)
\end{align}$
From the equations $\left( \text{a} \right),\left( \text{b} \right),\left( \text{c} \right),\left( \text{d} \right)$ we can say that options $\text{A,C}$ are the correct options.
Note: The students may make mistakes when they are taking the greatest integer of $-6.28$. The greatest Integer of $-6.28$ is $7$, don’t take it as $6$. If you take it as $6$, then the whole solution will be deflected from the correct way. You can also refer to the below picture to check the greatest integer values

Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

What is the difference between biodegradable and nonbiodegradable class 11 biology CBSE

Bond order ofO2 O2+ O2 and O22 is in order A O2 langle class 11 chemistry CBSE




