Question

If $f(x,y) = {({\text{max(}}x,y))^{{\text{min}}(x,y)}}$ and $g(x,y) = {\text{max}}(x,y) - \min (x,y)$ then Value of$f\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$ equals:

Answer 1

Hint:
If we are given that $f(x) = \max (1,2){\text{ then }}f(x) = 2$ because 2 is greater than 1. Similarly here we need to find the value of $\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$ and then we will find the value of $f\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$

Complete step by step solution:
Here we are given the two functions which are $f(x),g(x)$ and are defined as
$f(x,y) = {({\text{max(}}x,y))^{{\text{min}}(x,y)}}$
$g(x,y) = {\text{max}}(x,y) - \min (x,y)$
Here max and min are given so let us understand what is the meaning of max and min so if we are given that $f(x) = \max (x,y),x > y,{\text{ then }}f(x) = x$ because the maximum of the two values $x{\text{ and }}y$ is $x$and if we are given to find the value of $\min (x,y){\text{ then }}f(x) = y$ because it is minimum of the given two values in the function.
Let us explain by taking the graph and here $g(x){\text{ and }}f(x)$ are represented in the graph as

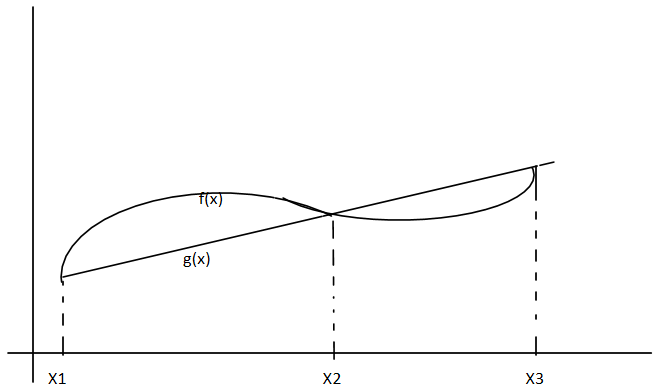
$f(x)$ is the curved line and $g(x)$ is the straight line intersecting at ${x_1},{x_2},{x_3}$
So for the condition that ${x_1} < x < {x_2}$ we know that $f(x) > g(x)$ then $\max (f(x),g(x)) = f(x)$ and $\min (f(x),g(x)) = g(x)$
Now for ${x_2} < x < {x_3}$ we know that $g(x) > f(x)$ then $\max (f(x),g(x)) = g(x)$ and $\min (f(x),g(x)) = f(x)$
Now we are given that $g(x,y) = {\text{max}}(x,y) - \min (x,y)$
We need to find the value of $\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$
So for $\left( {g\left( { - 1, - \dfrac{3}{2}} \right)} \right)$$ = \left( {\max g\left( { - 1, - \dfrac{3}{2}} \right) - \min g\left( { - 1, - \dfrac{3}{2}} \right)} \right)$
As $ - 1 > - \dfrac{3}{2}$ we can write that
$\left( {g\left( { - 1, - \dfrac{3}{2}} \right)} \right) = - 1 - ( - \dfrac{3}{2}) = \dfrac{1}{2}$
Now we need to find $g( - 4, - 1.75)$
$
   = \max ( - 4, - 1.75) - \min ( - 4, - 1.75) \\
   = - 1.75 - ( - 4) = 2.25 \\
 $
Now we need to find the value of $f\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$
Or we can say $f\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$$ = f(0.5,2.25)$
Now we know that it is defined that $f(x,y) = {({\text{max(}}x,4))^{{\text{min}}(x,4)}}$
$f(0.5,2.25) = {({\text{max(0}}{\text{.5}},2.25))^{{\text{min}}(0.5,2.25)}}$=${2.25^{0.5}} = \sqrt {\dfrac{{225}}{{100}}} = \dfrac{{15}}{{10}} = 1.5$

So we get that $f\left( {g\left( { - 1, - \dfrac{3}{2}} \right),g( - 4, - 1.75)} \right)$$ = 1.5$

Note:
So if the function is defined like $f(x)$ then for its being maximum and minimum the value of the derivative of it must be equal to zero which means that $f'(x) = 0$ so now if we get its double derivative as positive then it is the minimum and if it is negative then it is the maximum.