Question

If $f\left( x \right)=\min \left\{ \tan x,\cot x \right\},$ then
a) Range of f(x) is $(-\infty ,1]\cup \left( 0,1 \right)$
b) F is periodic function whose period is $\pi $
c) F is discontinuous at $x=\dfrac{n\pi }{2},n\in z$
d) F is not differentiable at $x=\dfrac{n\pi }{4},n\in z$

Answer 1

Hint: For solving this problem, we consider all the options individually and then analyse each option for its truth value as multiple answers are possible. We use the concept of minima in graph regions for analysing each option. First, we find the common part in the two graphs for a specific interval as both $\tan x\text{ and }\cot x$ are periodic and then we shade the minimum value for corresponding region to get minima. By doing so, we get the final result.

Complete step-by-step answer:
As per given the function is: $f\left( x \right)=\min \left\{ \tan x,\cot x \right\}$
To find the range of function f(x), we will use the graphical approach.
Draw the graph for tan x, cot x for all $x\in \left[ 0,\pi \right]$and that graph will give us range as they both are periodic functions with period $\pi $.

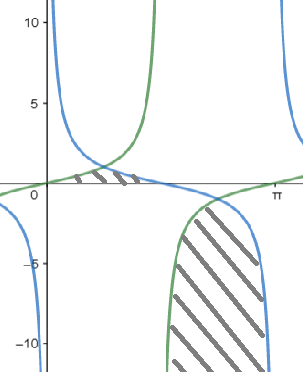
cot x = tan x
$\begin{align}
  & {{\tan }^{2}}x=1 \\
 & \Rightarrow \tan x=\pm 1 \\
\end{align}$
The value of tan x is 1 when the value of x is $\dfrac{\pi }{4},\dfrac{3\pi }{4}$.
Therefore, $x=\dfrac{\pi }{4},\dfrac{3\pi }{4}$ as $x\in \left[ 0,\pi \right]$
From the graph the darker lines give the required answer this range of f(x) is $(-\infty ,-1]\cup (0,1]$ as both tan x and cot x are periodic f(x) is periodic with period $\pi $.
So, option (a) and (b) are correct.
Now, considering option (c),
f(x) = min (tan x, cot x), and the periodicity of tan and cot function is $\pi $. Now, to obtain the periodicity of f(x):
\[\begin{align}
  & f\left( x+\pi \right)=\min \left( \tan \left( x+\pi \right),\cot \left( x+\pi \right) \right) \\
 & \because \tan \left( x+\pi \right)=\tan \left( x \right)\text{ and }\cot \left( x+\pi \right)=\cot \left( x \right) \\
 & \therefore f\left( \pi +x \right)=\min \left( \tan \left( x \right),\cot \left( x \right) \right) \\
 & \text{thus, }f\left( x \right)=f\left( x+\pi \right) \\
\end{align}\]
Hence, option (c) is also correct.
From graph we can see f(x) is discontinuous at point where $x=\dfrac{n\pi }{2},n\in z$ and as at points where $x=n\dfrac{\pi }{4},n\in z$ there exists a corner thus these are non- differentiable. So, option (d) is also correct.
Therefore, all the options are correct.

Note: The knowledge of the concept of minima for periodic function is must for solving this problem. Students must be careful while drawing the graph and should take the interval of periodicity carefully. All the options are analysed once the graph is formed.