Question

If $f\left( x \right)=a{{x}^{2}}+bx+c$ and a < 0. Now a point α lies between the two roots of the given expression, then which of the following is true.
$\begin{align}
  & \text{a) f(}\alpha \text{) will always be positive} \\
 & \text{b) f(}\alpha \text{) will always be negative} \\
 & \text{c) If both roots are negative then f(}\alpha \text{) will be negative}\text{.} \\
 & \text{d) If one root is negative and one root is positive then f(}\alpha \text{) will be negative } \\
\end{align}$

Answer 1

Hint: We know that for any quadratic equation $f\left( x \right)=a{{x}^{2}}+bx+c$ if a < 0 then the parabola is convex up parabola or downwards facing parabola. Now if we draw the graph of such parabola we can easily check the condition on f(x).

Complete step by step answer:
Now first let us consider the function $f\left( x \right)=a{{x}^{2}}+bx+c$
We know that the given equation is a quadratic equation and a quadratic equation represents a parabola.
Now the nature of parabola depends upon the constants a, b, c.
Now c here is the y intercept which determines where the parabola will intersect the y-axis.
By finding the discriminant of the equation we can determine the number of roots and hence the number of times the parabola cuts x-axis.
This discriminant is given by $D={{b}^{2}}-4ac$
Now D > 0 means that there are 2 roots hence the parabola will cut the x axis 2 times.
If D < 0 then we have the equation has no roots and hence it does not cut the x axis.
Now if D = 0 then we have the parabola just touches the x-axis.
Now a determines if the parabola is upwards facing or downwards facing.
If we have a < 0 then the parabola is downwards facing and if a > 0 then the parabola is upwards facing.
Now we are given with the fact that a < 0 and there are two roots.
Hence we know that the parabola is downwards facing the parabola with two roots.
Let us draw the graph of such parabola.

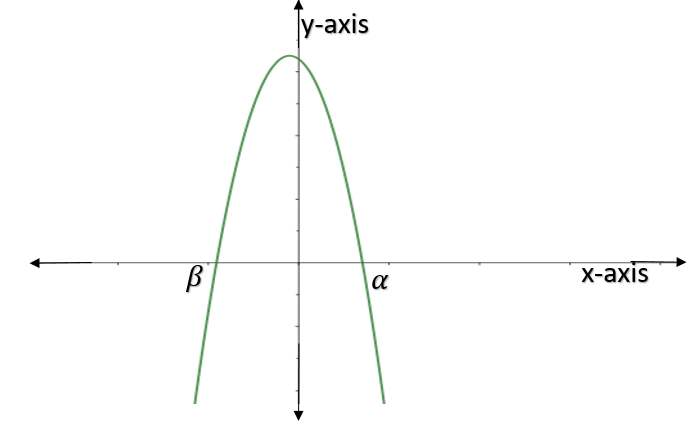
Hence we can see that between the roots we have the function is always positive.

So, the correct answer is “Option A”.

Note: Note that the fact that the function will be positive between the roots does not depend upon the nature of roots as we get a similar graph even if both roots are positive or negative. The function between the graph will always be above x-axis and hence will always be greater than 0.