Question

If $f:A\to B$ is a constant function which is onto then $B$ is
(a) a singleton set
(b) a null set
(c) an infinite set
(d) a finite set

Answer 1

Hint: To solve this problem, let us first understand what a function is, what a constant function is and what is the condition for a function to be onto.

Complete step-by-step answer:
A function is a process or a relation that associates each element $x$ of a set $X$ to a single element $y$ of another set $Y$ . Here $X$ is domain and $Y$ is co-domain of the function. The domain of a function is the set of possible inputs for the function. For example , the domain of $f\left( x \right)={{x}^{2}}$ is all real numbers, and the domain of $g\left( x \right)=\dfrac{1}{x}$ is all real numbers except for $x=0$ . Also, the co-domain of a function is the set into which all of the output of the function is constrained to fall. We can understand this by taking the example of $f\left( x \right)={{x}^{2}}$ .

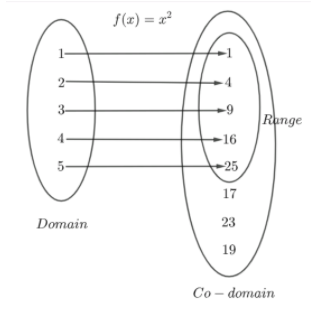
We can see that the domain of the function $f\left( x \right)={{x}^{2}}$ is the set $\left\{ 1,2,3,4,5 \right\}$ . Co-domain of the function $f\left( x \right)={{x}^{2}}$ is the set $\left\{ 1,4,9,16,25,17,23,19 \right\}$ . Here, we also have a range. So, let us know about range. A range is the set of all $f$ images of all the elements of domain.
According to the function $f\left( x \right)={{x}^{2}}$ , the set $\left\{ 1,4,9,16,25 \right\}$ is the range of the function $f\left( x \right)={{x}^{2}}$ .
Now, let us know about onto function. A function $f$ from a set $X$ to a set $Y$ is onto, if for every element $y$ in the co-domain $Y$ of $f$ , there is at least one element $x$ in the domain $X$ of $f$ such that $f\left( x \right)=y$ . We can also show it as
  

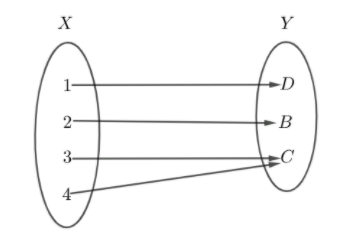
Here, we can see that each element of $X$ has a $f-image$ in $Y$ . We can also say that if a function is onto then the range set will be equal to the co-domain set.
Now, let us solve the given problem .
It is given that $f:A\to B$ is a constant function which is onto.
 $f:A\to B$ is a constant function means for each element in $A$ there is some $f-image$ in $B$ .
Also, $f:A\to B$ is onto which means $f\left( A \right)=B$ i.e. , range set is equal to domain set . Therefore we conclude that $B$ has only one element.
Thus, $B$ is a singleton set.
Hence the correct option is (a).

Note: Alternate shortcut:
$f\left( x \right)$ is a constant function $\Rightarrow $ Range of $f\left( x \right)$ is a singleton set.
For $f$to be an onto function, Co-domain $B$ should be equal to range.
 $\therefore B$ should be a singleton set.