Question

If f, g, and h are the lengths of the perpendicular from the circumcentre of triangle ABC on the sides a, b and c respectively. Prove that $\dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = \dfrac{1}{4}\dfrac{{abc}}{{fgh}}$.

Answer 1

Hint: We’ll initiate our solution using the theorem, the angle made at the circumcentre is double the angle of the remaining vertex. Then we’ll use the famous trigonometric identity $\tan A + \tan B + \tan C = \tan A\tan B\tan C$ to get the solution.

Complete step-by-step answer:
First of all, we’ll draw the diagram for a better understanding of the question batter.

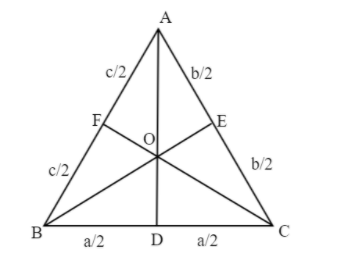
O is our circumcentre in the triangle.
Now, observe in the triangle OBD, OD is the given length f.
We need to somehow get $\dfrac{a}{f}$ so let’s consider, $\tan A$. One might think why $\tan A$ so it's because we knew that the angle made at the circumcentre is double the angle of the remaining vertex.
Now, $\tan A = \dfrac{a}{{2f}}$
So, $\dfrac{a}{f} = 2\tan A - - - - (1)$
Similarly, $\tan B = \dfrac{b}{{2g}}$ , which is nothing but $\dfrac{b}{g} = 2\tan B - - - - (2)$
And, in the end, $\tan C = \dfrac{c}{{2h}}$
So, $\dfrac{c}{h} = 2\tan C - - - (3)$

Keep this in mind, we have to prove that $\dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = \dfrac{1}{4}\dfrac{{abc}}{{fgh}}$
And we have got the value of $\dfrac{a}{f},\dfrac{b}{g},$ and $\dfrac{c}{h}$. By using them
$\begin{gathered}
  \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = 2\tan A + 2\tan B + 2\tan C \\
   \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = 2(\tan A + \tan B + \tan C) \\
\end{gathered} $
Here, we know that, $\tan A + \tan B + \tan C = \tan A\tan B\tan C$
Using this trigonometric identity
$\begin{gathered}
  \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = 2(\tan A + \tan B + \tan C) \\
   \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = 2(\tan A\tan B\tan C) \\
   \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = 2(\dfrac{a}{{2f}} \times \dfrac{b}{{2g}} \times \dfrac{c}{{2h}}) \\
   \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = 2(\dfrac{{abc}}{{8fgh}}) \\
   \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = \dfrac{1}{4}\dfrac{{abc}}{{fgh}} \\
\end{gathered} $

Hence proved.

Note: Those who are interested in $\tan A + \tan B + \tan C = \tan A\tan B\tan C$ for any triangle, can prove this in the following way. In the triangle, we know, $\angle A + \angle B + \angle C = \pi $. Taking C to the right-hand side and then tab both sides we’ll get
$\begin{gathered}
  \tan (A + B) = \tan (\pi - C) \\
   \Rightarrow \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}} = - \tan C \\
   \Rightarrow \tan A + \tan B = - \tan C + \tan A\tan B\tan C \\
   \Rightarrow \tan A + \tan B + \tan C = \tan A\tan B\tan C \\
\end{gathered} $