
If cos(t) = $-\dfrac{7}{8}$ with $\pi \le t\le 3\dfrac{\pi }{2}$, how do you find the value of sin(2t)?
Answer
555k+ views
Hint: In this problem, we will need identities for solving and calculating the value for sin(2t) if the value of cos(t) is provided as $-\dfrac{7}{8}$. Cos(t) is negative because it lies in the third quadrant in the coordinate plane. You need to know the signs for different quadrants for both sin(t) and cos(t). Identities used to solve the question are:
$\Rightarrow $sin2x = 2sinxcosx
$\Rightarrow {{\cos }^{2}}x+{{\sin }^{2}}x=1$
Complete step-by-step answer:
Let’s discuss the question now.
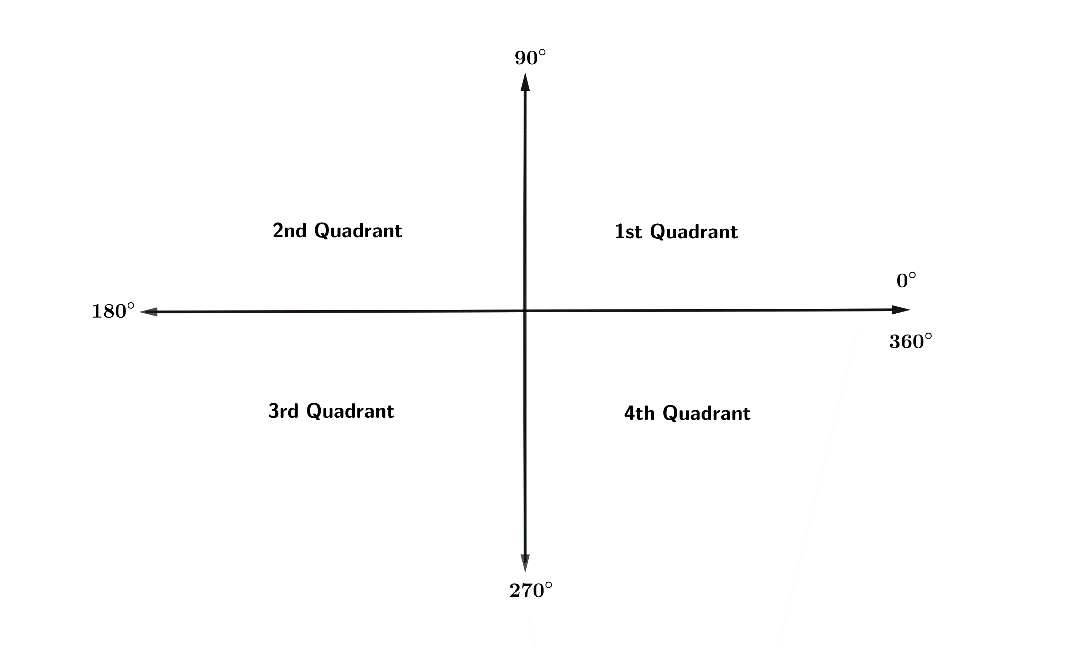
From the above plane, we can see that:
Angles of the first quadrant lie in $0 < \theta < 90$ and the values of x and y both are positive.
Similarly for the second quadrant, angles lie in $90 < \theta < 180$ where the values of x are negative and y are positive.
In the third quadrant, angles lie in $180 < \theta < 270$. The values of x and y both are negative.
Fourth quadrant consists of the angles which lie in $270 < \theta < 360$. The values of x are positive whereas y are negative.
Let’s see the trigonometric values for sin and cos for different quadrants:
In this question, cos(t) is given negative according to the range $\pi \le t\le 3\dfrac{\pi }{2}$. In the third quadrant, the value of cos$\left( \theta \right)$ is –ve.
Formula for sin2t = 2sintcost
For this, we are given cos(t) but sint(t) is not given. So first we will find the value for sin(t). as we know that:
$\Rightarrow {{\cos }^{2}}x+{{\sin }^{2}}x=1$
Then,
$\Rightarrow {{\sin }^{2}}x=1-{{\cos }^{2}}x$
So, sin(t) will be:
$\Rightarrow \sin t=\sqrt{1-{{\cos }^{2}}t}$
Now put the values of cos(t) in above equation:
$\Rightarrow \sin t=\sqrt{1-{{\left( \dfrac{-7}{8} \right)}^{2}}}$
Open brackets and we get:
$\Rightarrow \sin t=\sqrt{1-\dfrac{49}{64}}$
Solve the under root and we get:
$\Rightarrow \sin t=\sqrt{\dfrac{64-49}{64}}\Leftrightarrow \sin t=\sqrt{\dfrac{15}{64}}$
Remove the root now and we have:
$\therefore \sin t=\dfrac{\sqrt{15}}{8}$
Now put this value of sin(t) in the formula of sin(2t):
$\Rightarrow $sin2t = 2sin(t)cos(t)
As sin(t) lies in the the third quadrant so we put –ve sign before it:
$\sin (2t)=2\times \left( -\dfrac{\sqrt{15}}{8} \right)\times \left( -\dfrac{7}{8} \right)$
Multiply all the values, we get:
$\sin (2t)=\left( \dfrac{7\sqrt{15}}{32} \right)$
Use $\sqrt{15}=3.87$ in above value:
$\Rightarrow \sin (2t)=\left( \dfrac{7\times 3.87}{32} \right)$
$\therefore \sin (2t)=0.85$
This is the final answer.
Note: You should know all the trigonometric identities and properties before solving any question related to trigonometry. And also, learn the square and square roots of the numbers so that there should be no need to find the LCM and then form pairs to check the squares or square root.
$\Rightarrow $sin2x = 2sinxcosx
$\Rightarrow {{\cos }^{2}}x+{{\sin }^{2}}x=1$
Complete step-by-step answer:
Let’s discuss the question now.

From the above plane, we can see that:
Angles of the first quadrant lie in $0 < \theta < 90$ and the values of x and y both are positive.
Similarly for the second quadrant, angles lie in $90 < \theta < 180$ where the values of x are negative and y are positive.
In the third quadrant, angles lie in $180 < \theta < 270$. The values of x and y both are negative.
Fourth quadrant consists of the angles which lie in $270 < \theta < 360$. The values of x are positive whereas y are negative.
Let’s see the trigonometric values for sin and cos for different quadrants:
| Trigonometric function | First quadrant | Second quadrant | Third quadrant | Fourth quadrant |
| sin$\left( \theta \right)$ | +ve | +ve | -ve | -ve |
| cos$\left( \theta \right)$ | +ve | -ve | -ve | +ve |
In this question, cos(t) is given negative according to the range $\pi \le t\le 3\dfrac{\pi }{2}$. In the third quadrant, the value of cos$\left( \theta \right)$ is –ve.
Formula for sin2t = 2sintcost
For this, we are given cos(t) but sint(t) is not given. So first we will find the value for sin(t). as we know that:
$\Rightarrow {{\cos }^{2}}x+{{\sin }^{2}}x=1$
Then,
$\Rightarrow {{\sin }^{2}}x=1-{{\cos }^{2}}x$
So, sin(t) will be:
$\Rightarrow \sin t=\sqrt{1-{{\cos }^{2}}t}$
Now put the values of cos(t) in above equation:
$\Rightarrow \sin t=\sqrt{1-{{\left( \dfrac{-7}{8} \right)}^{2}}}$
Open brackets and we get:
$\Rightarrow \sin t=\sqrt{1-\dfrac{49}{64}}$
Solve the under root and we get:
$\Rightarrow \sin t=\sqrt{\dfrac{64-49}{64}}\Leftrightarrow \sin t=\sqrt{\dfrac{15}{64}}$
Remove the root now and we have:
$\therefore \sin t=\dfrac{\sqrt{15}}{8}$
Now put this value of sin(t) in the formula of sin(2t):
$\Rightarrow $sin2t = 2sin(t)cos(t)
As sin(t) lies in the the third quadrant so we put –ve sign before it:
$\sin (2t)=2\times \left( -\dfrac{\sqrt{15}}{8} \right)\times \left( -\dfrac{7}{8} \right)$
Multiply all the values, we get:
$\sin (2t)=\left( \dfrac{7\sqrt{15}}{32} \right)$
Use $\sqrt{15}=3.87$ in above value:
$\Rightarrow \sin (2t)=\left( \dfrac{7\times 3.87}{32} \right)$
$\therefore \sin (2t)=0.85$
This is the final answer.
Note: You should know all the trigonometric identities and properties before solving any question related to trigonometry. And also, learn the square and square roots of the numbers so that there should be no need to find the LCM and then form pairs to check the squares or square root.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

What is the difference between biodegradable and nonbiodegradable class 11 biology CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE




