Question

If \[\cos ec\left( {{{\tan }^{ - 1}}(\cos ({{\cot }^{ - 1}}(\sec ({{\sin }^{ - 1}}a))))} \right) = \sqrt {p - {a^q}} \] , where $ ac[0,1]. $
Find the value of $ p + q $ .

Answer 1

Hint: We have to find the value of $ p + q $ . For this we take the left hand side of the expression. We have to solve $ {\sin ^{ - 1}}a $ . We convert $ {\sin ^{ - 1}}a $ into $ {\sec ^{ - 1}} $ function once we have close, we convert $ {\cot ^{ - 1}} $ function into $ {\cos ^{ - 1}} $ function. After that we convert $ {\tan ^{ - 1}} $ function into $ \cos e{c^{ - 1}} $ function. At the last we left with a value which will be free from inverse trigonometric function. Then we equate this value with the right hand side.

Complete step by step solution:
We have given that \[\cos ec\left( {{{\tan }^{ - 1}}(\cos ({{\cot }^{ - 1}}(\sec ({{\sin }^{ - 1}}a))))} \right) = \sqrt {p - {a^q}} \] where $ ac[0,1] $
We have to calculate the value of $ p + q $
L.H.S. = \[\cos ec\left( {{{\tan }^{ - 1}}(\cos ({{\cot }^{ - 1}}(\sec ({{\sin }^{ - 1}}a))))} \right)\]
We have to convert $ {\sin ^{ - 1}} $ function into $ {\sec ^{ - 1}} $ function.
Let: $ {\sec ^{ - 1}}a = \theta $
 $ a = \sec \theta $
We know that \[{\sin ^2}\theta + {\cos ^2}\theta = 1\]
 \[ \Rightarrow {\cos ^2}\theta = 1 - {\sin ^2}\theta \]
 \[ \Rightarrow \cos \theta = \sqrt {1 - {{\sin }^2}\theta } \]
Also \[\dfrac{1}{{\cos \theta }} = \dfrac{1}{{\sqrt {1 - {{\sin }^2}\theta } }}\]
 \[ \Rightarrow \] \[\theta = {\sec ^{ - 1}}\left( {\dfrac{1}{{\sqrt {1 - {{\sin }^2}\theta } }}} \right)\]
 \[ = \sec \theta \left( {\dfrac{1}{{\sqrt {1 - {a^2}} }}} \right)\]
So, L.H.S. \[ = \cos ec\left( {{{\tan }^{ - 1}}(\cos ({{\cot }^{ - 1}}(\sec ({{\sin }^{ - 1}}\dfrac{1}{{\sqrt {1 - {a^2}} }}))))} \right)\]
 \[ = \cos ec\left( {{{\tan }^{ - 1}}(\cos ({{\cot }^{ - 1}}(\dfrac{1}{{\sqrt {1 - {a^2}} }})))} \right)\]
Now we convert \[{\cot ^{ - 1}}\] function into \[{\cos ^{ - 1}}\] function
We will to it will the help of right angle triangle.

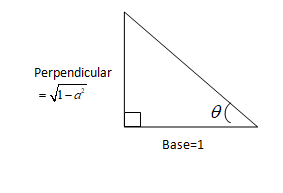
 \[{\cot ^{ - 1}}\left( {\dfrac{1}{{\sqrt {1 - {a^2}} }}} \right) = \theta \]
 \[\cot \theta = \dfrac{1}{{\sqrt {1 - {a^2}} }}\]
We know that \[\cot \theta = \dfrac{{Base}}{{Perpendicular}}\]
By Pythagoras theorem
 \[ \Rightarrow \] $ {\left( {Hypotenuse} \right)^2} = {\left( {Base} \right)^2} + {\left( {Perpendicular} \right)^2} $
 \[ \Rightarrow \] \[{\left( {Hypotenuse} \right)^2} = {\left( 1 \right)^2} + {\left( {\sqrt {1 - {a^2}} } \right)^2}\]
 \[ \Rightarrow \] \[{\left( {Hypotenuse} \right)^2} = 1 + 1 - {a^2}\]
 \[ \Rightarrow \] \[{\left( {Hypotenuse} \right)^2} = 2 - {a^2}\]
 \[ \Rightarrow \] \[Hypotenuse = \sqrt {2 - {a^2}} \]
Therefore value of \[\cos \theta = \dfrac{{Base}}{{Hypotenuse}}\]
 \[ \Rightarrow \] \[\cos \theta = \dfrac{1}{{\sqrt {2 - {a^2}} }}\]
 \[ \Rightarrow \] \[\theta = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt {2 - {a^2}} }}} \right)\]
So L.H.S. \[ = \cos ec\left( {{{\tan }^{ - 1}}(\cos ({{\cos }^{ - 1}}(\dfrac{1}{{\sqrt {2 - {a^2}} }})))} \right)\]
 \[ = \cos ec\left( {{{\tan }^{ - 1}}(\dfrac{1}{{\sqrt {2 - {a^2}} }})} \right)\]
Now we convert \[{\tan ^{ - 1}}\] function into \[\cos e{c^{ - 1}}\] function
Let $ {\tan ^{ - 1}}\dfrac{1}{{\sqrt {2 - {a^2}} }} = \theta $
 \[ \Rightarrow \] $ \tan \theta = \dfrac{1}{{\sqrt {2 - {a^2}} }} $
Also we know that $ \tan \theta = \dfrac{{Perpendicular}}{{Base}} $
Perpendicular $ = 1 $
Base $ = \sqrt {2 - {a^2}} $
 \[ \Rightarrow \] $ {\left( {Hypotenuse} \right)^2} = {\left( {Perpendicular} \right)^2} + {\left( {Base} \right)^2} $
 \[ \Rightarrow \] \[{\left( {Hypotenuse} \right)^2} = {\left( 1 \right)^2} + {\left( {\sqrt {2 - {a^2}} } \right)^2}\]
 \[ \Rightarrow \] \[{\left( {Hypotenuse} \right)^2} = 1 + 2 - {a^2}\]
Here we use addition then it will become \[3\]
 \[ \Rightarrow \] \[{\left( {Hypotenuse} \right)^2} = 3 - {a^2}\]
 \[ \Rightarrow \] \[Hypotenuse = \sqrt {3 - {a^2}} \]
So we have \[\cos ec\theta = \dfrac{{Hypotenuse}}{{Base}}\] \[ = \dfrac{{\sqrt {3 - {a^2}} }}{1}\]
 \[ \Rightarrow \] \[\cos ec\theta = \sqrt {3 - {a^2}} \]
 \[ \Rightarrow \] \[\theta = \cos e{c^{ - 1}}\left( {\sqrt {3 - {a^2}} } \right)\]
Therefore L.H.S. \[ = \cos ec\left( {\cos e{c^{ - 1}}\left( {\sqrt {3 - {a^2}} } \right)} \right)\]
L.H.S. \[ = \sqrt {3 - {a^2}} \]
Now we compare the left hand side with the right hand side.
 \[ \Rightarrow \sqrt {3 - {a^2}} = \sqrt {p - {a^2}} \]
 \[ \Rightarrow 3 - {a^2} = p - {a^2}\]
From above we get \[p = 3\] and \[q = 2\]
So value of \[p + q = 3 + 2 = 5\]
 \[p + q = 5\]

So, the correct answer is “Option C”.

Note: In mathematics, inverse trigonometric functions are inverse of the trigonometric functions. Specifically they are inverse of sine, cosine, tangent, cotangent, secant and cosecant functions. They are used to obtain an angle from any of the angle’s trigonometric operation of the trigonometric functions.