Question

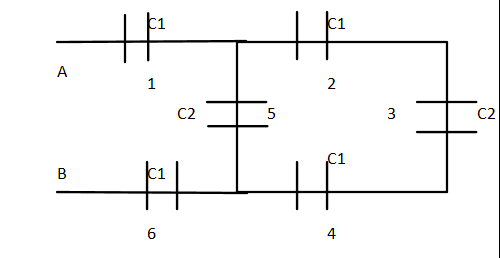
If \[C1 = 3pF\]and\[C2 = 2pF\]. Calculate the equivalent capacitance of a given circuit.

Answer 1

Hint:As we know the when capacitance are in series in any circuit theses are added inversely that is using the formula \[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}\]but if we these are in parallel these are added directly and then we can calculate the equivalent capacitance.

Complete step-by-step solution:
In the given question we are given with two capacitances as, \[C1 = 3pF\]and\[C2 = 2pF\]
And these are joined in given circuit above
So we can see the right loop in circuit where three capacitances are joined in series, therefore equivalent capacitance of this side of loop will be,
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_1}}}\]
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{3} + \dfrac{1}{2} + \dfrac{1}{3}\]
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{2}{3} + \dfrac{1}{2}\]
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{7}{6}\]
\[{C_{eq}} = \dfrac{6}{7}\], now this equivalent capacitance will be in parallel with point \[5\] in circuit so equivalent capacitance of this will be
\[{C_{eq}} = \dfrac{6}{7} + 2\]
\[{C_{eq}} = \dfrac{{20}}{7}\], now this equivalent capacitance will be in series with points \[6\]and \[1\]
So it equivalent capacitance and final capacitance can be calculated as
\[\dfrac{1}{{{C_{final}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_{eq}}}} + \dfrac{1}{{{C_1}}}\]
\[\dfrac{1}{{{C_{final}}}} = \dfrac{7}{{20}} + \dfrac{2}{3}\]
\[\dfrac{1}{{{C_{final}}}} = \dfrac{{61}}{{60}}\]
\[{C_{final}} = \dfrac{{60}}{{61}}\].
Therefore the correct answer is \[{C_{final}} = \dfrac{{60}}{{61}}\].

Additional information: As above in the question there are just empty di capacitors that means there was nothing inside the capacitor but sometimes there is slab known as dielectric that is used to store more charge in the same potential difference around capacitor because electric field present on dielectric slab will cancel electric field around the capacitor plates due to charge present and it also helps to sustain greater potential difference around the capacitor plates which will help it to store more charge and energy on capacitor.

Note:- In the given circuit don’t mistakenly mix series and parallel capacitance as the formula is opposite to resistance as in resistance if resistors are in series they are added directly and nor inversely.