Question

If \[{C_1} = 3\,pF\]and \[{C_2} = 2\,pF\], calculate the equivalent capacitance of the network shown in the figure between points A and B?

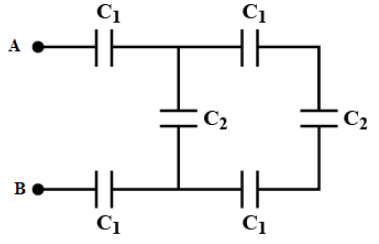
(A) 1 pF
(B) 2 pF
(C) 3 pF
(D) 4 pF

Answer 1

Hint: Identify which capacitors are connected in series and use the formula for equivalent capacitance for series combination. This series combination of capacitors may be parallel to the other capacitors. Draw the simplified circuit if needed.

Formula used:
The formula for equivalent capacitance in the parallel combination is,
\[{C_{eq}} = {C_1} + {C_2} + ...\]
Also, the formula for equivalent capacitance in the series combination of capacitors is,
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ...\]

Complete step by step answer:
We draw the above circuit diagram by labeling the capacitors for the ease in identification as shown in the figure below.

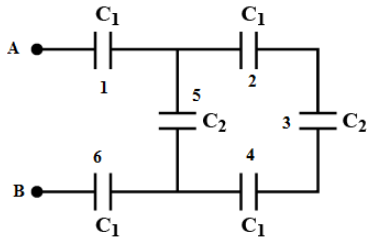
In the above figure, we can see the capacitors 2, 3 and 4 are in series. Therefore, the equivalent capacitance of these capacitors is,
\[\dfrac{1}{{{C_{234}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_1}}}\]
We substitute \[{C_1} = 3\,pF\]and \[{C_2} = 2\,pF\] in the above equation.
\[\dfrac{1}{{{C_{234}}}} = \dfrac{1}{3} + \dfrac{1}{2} + \dfrac{1}{3}\]
\[ \Rightarrow \dfrac{1}{{{C_{234}}}} = \dfrac{1}{3} + \dfrac{1}{2} + \dfrac{1}{3}\]
\[ \Rightarrow \dfrac{1}{{{C_{234}}}} = \dfrac{7}{6}\]
\[ \Rightarrow {C_{234}} = \dfrac{6}{7}\,{\text{pF}}\]
Now, the capacitance \[{C_{234}}\] is in parallel with the capacitor 5. Therefore, we can calculate the equivalent capacitance as follows,
\[{C_{2345}} = {C_2} + {C_{234}}\]
We substitute \[\dfrac{6}{7}\,{\text{pF}}\] for \[{C_{234}}\] and \[2\,pF\] for \[{C_2}\] in the above equation.
\[ \Rightarrow {C_{2345}} = 2 + \dfrac{6}{7}\]
\[ \Rightarrow {C_{2345}} = \dfrac{{20}}{7}\,{\text{pF}}\]
Now, we see the capacitors 1, 6 and the capacitance \[{C_{2345}}\] are in series as shown in the figure below.

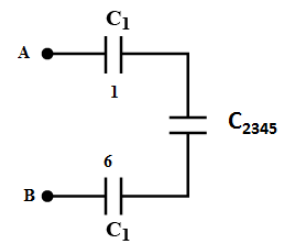
We can calculate the equivalent capacitance for the above arrangement of capacitance as follows,
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_{2345}}}} + \dfrac{1}{{{C_1}}}\]
We substitute \[{C_1} = 3\,pF\] and \[{C_{2345}} = \dfrac{{20}}{7}\,{\text{pF}}\] in the above equation.
\[\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{3} + \dfrac{1}{{\dfrac{{20}}{7}}} + \dfrac{1}{3}\]
\[ \Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{3} + \dfrac{7}{{20}} + \dfrac{1}{3}\]
\[ \Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{{61}}{{60}}\]
\[ \Rightarrow {C_{eq}} = \dfrac{{60}}{{61}}\,pF\]
\[ \therefore {C_{eq}} \approx 1\,pF\]

Therefore, the equivalent capacitance between point A and B is 1 pF.So the correct answer is option (A).

Note: The formula for equivalent capacitance and equivalent resistance are different for series and parallel combination. Most of the time, students use formula for equivalent resistance to determine the equivalent capacitance. Note that, formula for equivalent capacitance in series combination is similar to the formula for equivalent resistance in parallel combination. To determine the equivalent capacitance, students don’t need to convert the unit into farad if not necessary.