Question

If an AC main supply is given to be $ 220V $, the average emf during a positive half cycle will be
   $ \begin{align}
  & A)198V \\
 & B)220V \\
 & C)240V \\
 & D)220\sqrt{2}V \\
\end{align} $

Answer 1

Hint: Average voltage during a positive cycle can be defined as the average of instantaneous values along the time axis for the positive half cycle. We must know that average voltage is proportional to the maximum applied voltage. Maximum voltage is given as $ \sqrt{2} $ times the rms voltage. The voltage in supply lines is usually rms voltage.

Formula used:
$ {{V}_{avg}}=\dfrac{2}{\pi }{{V}_{\max }} $

Complete step-by-step answer:
We know that the magnitude of voltage through an AC main supply is usually rms voltage. If we need to find the maximum voltage during a half cycle, we must multiply the incoming rms voltage with $ \sqrt{2} $ . i.e.
 $ {{V}_{\max }}=\sqrt{2}{{V}_{rms}} $
Here, $ {{V}_{rms}} $ is given as $ 220V $ , so the maximum amplitude of the voltage in the positive half cycle will be,
 $ {{V}_{\max }}=\sqrt{2}\times 220=220\sqrt{2}V $
If we represent one full cycle of an AC voltage, it will be like,

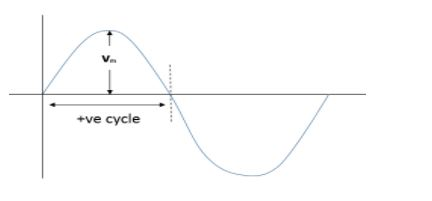
Now, the average velocity of an AC voltage supply during its positive cycle is directly proportional to the peak value which we had already found. That is,
 $ \begin{align}
  & {{V}_{avg}}=\dfrac{2}{\pi }{{V}_{\max }} \\
 & {{V}_{avg}}=\dfrac{2}{3.14}\times 220\sqrt{2}\approx 198V \\
\end{align} $
Therefore, we have found the average voltage of an AC mains during the positive half cycle, which is having $ 220V $ input voltage to be $ 198V $ .

So, the correct answer is “Option A”.

Note: We can solve this question easily by multiplying the given input voltage, which is $ {{V}_{rms}} $ with 0.9. This constant is obtained from the expression $ {{V}_{avg}}=\dfrac{2}{\pi }.\sqrt{2}{{V}_{rms}} $ . We will take out the constant and evaluate them. i.e. $ k=\dfrac{2}{\pi }.\sqrt{2}\approx 0.9 $ . So it will be very easy for us to find the average velocity if input velocity is given in the question.