Question

If $a\cdot b=0$ and $a+b$ makes an angle of ${{60}^{\circ }}$ with $b$ then $\left| a \right|$ is equal to
$\left( A \right)\text{ 0}$
$\left( B \right)\text{ }\dfrac{1}{\sqrt{3}}\left| b \right|$
$\left( C \right)\text{ }\dfrac{1}{\left| b \right|}$
$\left( D \right)\text{ }\left| b \right|$
$\left( E \right)\text{ }\sqrt{3}\left| b \right|$

Answer 1

Hint: In this question we have been given with two vectors which are $a$ and $b$. We have to find the value of $\left| a \right|$ given that $a\cdot b=0$ and $a+b$ makes an angle of ${{60}^{\circ }}$. We will use the property of dot product of vectors to find the all the angles in the triangle, we will then use trigonometric properties to get the relationship with the sides and get the required value of $\left| a \right|$.

Complete step by step answer:
We know that $a\cdot b=0$, which represents the dot product of vectors. We know that the dot product of perpendicular vectors is always zero. Which implies that since $a\cdot b=0$, $a$ is perpendicular to $b$. Mathematically it can be written as $a\bot b$.
This implies that the vectors $a,b$ and $a+b$ which is the resultant vector, form a right-angled triangle.
Consider the triangle to be $\Delta PQR$, we have the triangle as:

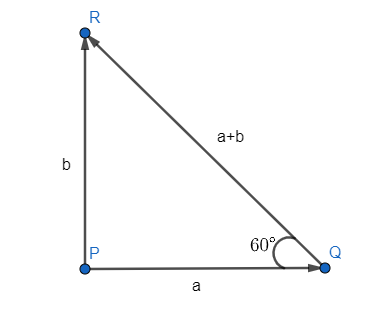
Now we know that $\tan \theta =\dfrac{perpendicular}{base}$ therefore, in $\Delta PQR$, we have:
$\Rightarrow \tan {{60}^{\circ }}=\dfrac{\left| a \right|}{\left| b \right|}$
Now we know that the value of $\tan {{60}^{\circ }}=\sqrt{3}$ therefore, on substituting, we get:
$\Rightarrow \sqrt{3}=\dfrac{\left| a \right|}{\left| b \right|}$
On transferring the term $\left| b \right|$ from the right-hand side to the left-hand side, we get:
$\Rightarrow \sqrt{3}\left| b \right|=\left| a \right|$
On rearranging, we get:
$\Rightarrow \left| a \right|=\sqrt{3}\left| b \right|$, which is the required value of $\left| a \right|$
So, the correct answer is “Option E”.

Note: It is to be remembered that modulus sign is used in representing the value since the value of vectors cannot be negative. The dot product in vectors represents the amount of which one vector goes in the direction of another vector. It is to be noted that vector dot product and cross product are two different things.