Question

If ABCDEF is a regular hexagon, then show that \[\overrightarrow{AD}+\overrightarrow{EB}+\overrightarrow{FC}\] equals to \[4\overrightarrow{AB}.\]

Answer 1

Hint: To solve this question, we will first draw the hexagon and draw its direction clockwise and then join all the diagonals. Finally, we will use the property of the regular hexagon stated as “All diagonals length of the hexagon is twice the length of its parallel sides”.

Complete step-by-step solution:
Let us draw the regular hexagon first. A hexagon means 6 sided polygon. Here, the vertices are named as A, B, C, D, E, F, then we have the hexagon as

Let us join all the points to each other to get \[\overrightarrow{AD},\overrightarrow{EB},\overrightarrow{FC},etc.\] and also draw the direction of lines in the clockwise motion. Doing so, we have,

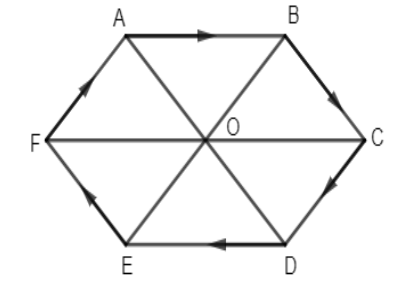
Let O be the center point. As we have to find the sum of \[\overrightarrow{AD},\overrightarrow{EB},\overrightarrow{FC},\] so let us first get the direction of \[\overrightarrow{AD},\overrightarrow{EB},\overrightarrow{FC}.\] \[\overrightarrow{AD}\] will be in the direction starting from A going to D. \[\overrightarrow{EB}\] will be in the direction starting from E going to B and \[\overrightarrow{FC}\] will be in the direction starting from F going to C. We have the figure as,

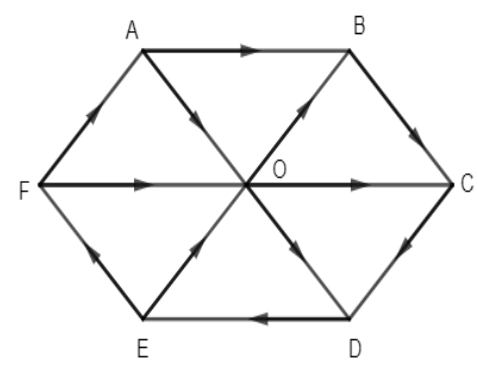
Now, as we are given the regular hexagon. A regular hexagon has a property that the length of the diagonal is twice the length of its parallel sides. Using this property, we can say, AD Diagonal is 2BC.
\[\Rightarrow AD=2BC.....\left( i \right)\]
Now because \[\overrightarrow{EB}\] is also diagonal, then using the same property of the regular hexagon, we have,
\[\overrightarrow{EB}=2\overrightarrow{FA}....\left( ii \right)\]
Similarly, \[\overrightarrow{FC}\] is again a diagonal of the given regular hexagon.
\[\overrightarrow{FC}=2\overrightarrow{AB}....\left( iii \right)\]
Now, let us add equation (i) and (ii) to get \[\overrightarrow{AD}+\overrightarrow{EB}.\]
\[\Rightarrow \overrightarrow{AD}+\overrightarrow{EB}=2\overrightarrow{BC}+2\overrightarrow{FA}\]
Now using the above stated property, we have that half of the diagonal is equal to the length of the sides of the regular hexagon.
\[\Rightarrow \overrightarrow{BC}=\overrightarrow{AO}\]
\[\Rightarrow \overrightarrow{AD}+\overrightarrow{EB}=2\left( \overrightarrow{BC}+\overrightarrow{FA} \right)\]
Using \[\overrightarrow{BC}=\overrightarrow{AO}\] we have,
\[\Rightarrow \overrightarrow{AD}+\overrightarrow{EB}=2\left( \overrightarrow{AO}+\overrightarrow{FA} \right).....\left( iv \right)\]
Now consider the triangle AOF, then in a triangle, if all the sides of the triangle are taken in order, the sum of all vectors = 0. Applying this in triangle AOF, we get,
In triangle AOF,
\[\overrightarrow{AO}+\overrightarrow{FA}+\overrightarrow{OF}=0\]
\[\Rightarrow \overrightarrow{AO}+\overrightarrow{FA}=-\overrightarrow{OF}.....\left( v \right)\]
Now substitute the value of equation (v) in equation (iv), we get,
\[\Rightarrow \overrightarrow{AD}+\overrightarrow{EB}=-2\overrightarrow{OF}\]
Now because \[\overrightarrow{PQ}=-\overrightarrow{QP},\] which is taken in the opposite direction.
\[\Rightarrow -2\overrightarrow{OF}=2\overrightarrow{FO}\]
\[\Rightarrow \overrightarrow{AD}+\overrightarrow{EB}+2\overrightarrow{FO}\]
Now \[\overrightarrow{FO}=\overrightarrow{AB}\] using the above-stated property of the regular hexagon.
\[\Rightarrow \overrightarrow{AD}+\overrightarrow{EB}=2\overrightarrow{AB}.....\left( vi \right)\]
Finally from equation (iii) and (vi), we have,
\[\overrightarrow{AD}+\overrightarrow{EB}+\overrightarrow{FC}=2\overrightarrow{AB}+2\overrightarrow{AB}=4\overrightarrow{AB}\]
Hence proved.

Note: Always in the case of vector, remember that the vector value changes if taken in the opposite or wrong direction, A vector is given as \[\overrightarrow{AB}.\]

This is not equal to \[\overrightarrow{BA}\] as \[\overrightarrow{AB}=-\overrightarrow{BA}.\] \[-\overrightarrow{BA}\] is nothing but the vector the same magnitude as \[\overrightarrow{AB}\] in the opposite direction.